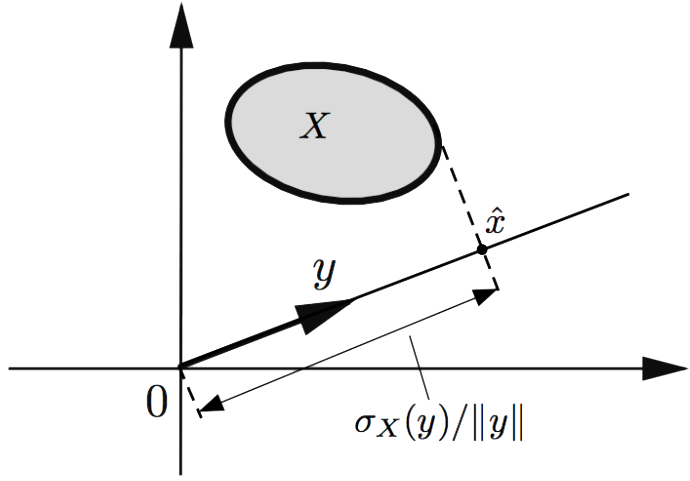
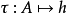基本介紹
- 中文名:支撐函式
- 外文名:support function
- 學科:數學
- 屬性:描述了支撐原始集的超平面的距離
- 性質:唯一確定封閉凸集
- 相關名詞:閔可夫斯基加法
簡介,定義,舉例,屬性,作為x的函式,作為A的函式,
簡介
在數學中,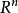 中的非空閉合凸集A的支撐函式
中的非空閉合凸集A的支撐函式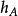 描述了支撐原始集A的超平面的距離。 支撐函式是
描述了支撐原始集A的超平面的距離。 支撐函式是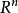 上的凸函式。 任何非空的封閉凸集A由
上的凸函式。 任何非空的封閉凸集A由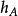 唯一確定。 此外,作為集合A的函式的支撐函式與許多幾何操作相兼容,例如縮放,平移,旋轉和閔可夫斯基加法。 由於這些屬性,支撐函式是凸幾何中最重要的基本概念之一。
唯一確定。 此外,作為集合A的函式的支撐函式與許多幾何操作相兼容,例如縮放,平移,旋轉和閔可夫斯基加法。 由於這些屬性,支撐函式是凸幾何中最重要的基本概念之一。
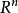
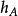
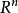
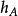
定義
支撐函式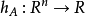 中的非空封閉凸集A由下式確定:
中的非空封閉凸集A由下式確定:
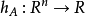
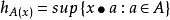
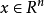
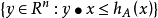
並且在這個半空間的邊界中至少有一個A點
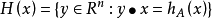
因此,超平面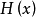 稱為具有外部(或外部)單位法向量x的支撐超平面。 外部這個詞在這裡很重要,因為x的方向起作用,所以集合
稱為具有外部(或外部)單位法向量x的支撐超平面。 外部這個詞在這裡很重要,因為x的方向起作用,所以集合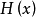 通常不同於
通常不同於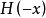 。 現在
。 現在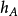 是
是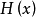 與原點的(有符號)距離。
與原點的(有符號)距離。
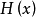
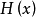
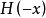
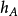
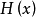
舉例
A = {a}的支撐函式是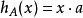 。
。
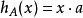
歐幾里得單位球B1的支撐函式是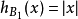 。
。
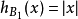
如果A是具有端點-a的原點的線段,則A是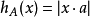 。
。
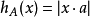
屬性
作為x的函式
緊湊凸集的支撐函式是實值和連續的,但是如果集合是無界的,則其支撐函式被擴展為實值(它的值為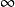 )。 由於任何非空閉合凸集是其支撐半空間的交集,所以函式
)。 由於任何非空閉合凸集是其支撐半空間的交集,所以函式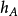 唯一地確定A。 這可以用於分析描述凸集的某些幾何屬性。 例如,如果且僅
唯一地確定A。 這可以用於分析描述凸集的某些幾何屬性。 例如,如果且僅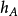 是偶函式,則集合A相對於原點是點對稱的。
是偶函式,則集合A相對於原點是點對稱的。
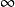
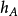
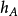
一般來說,支持功能是不可區分的。 然而,定嚮導數存在並產生支持集的支持功能。 如果A是緊湊且凸的,並且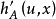 表示方向x上u≠0的
表示方向x上u≠0的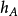 的方嚮導數,我們有
的方嚮導數,我們有
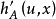
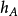
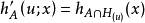
這裡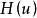 是上面定義的具有外部法向量u的A的支撐超平面。 如果
是上面定義的具有外部法向量u的A的支撐超平面。 如果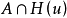 是單例
是單例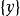 ,則說明支撐函式在u處是可微分的,其梯度與y重合。 相反,如果
,則說明支撐函式在u處是可微分的,其梯度與y重合。 相反,如果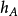 在u是可微分的,則
在u是可微分的,則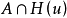 是單例的。 因此,若且唯若A嚴格為凸(A的邊界不包含任何線段)時,
是單例的。 因此,若且唯若A嚴格為凸(A的邊界不包含任何線段)時,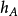 在所有點u≠0時是可微分的。
在所有點u≠0時是可微分的。
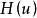
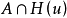
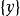
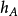
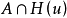
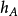
它的定義直接遵循支持函式是正同質的:
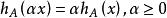
和

因此,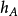 是凸函式。 在凸幾何中,這些屬性表征支撐函式是至關重要的:
是凸函式。 在凸幾何中,這些屬性表征支撐函式是至關重要的: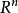 上的任何正齊次、凸實值函式是非空緊湊凸集。 已知有幾個證明,一個正在使用的事實是,正均勻、凸實值函式的勒讓德變換是緊湊凸集的(凸)指標函式。
上的任何正齊次、凸實值函式是非空緊湊凸集。 已知有幾個證明,一個正在使用的事實是,正均勻、凸實值函式的勒讓德變換是緊湊凸集的(凸)指標函式。
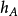
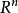
許多作者將支撐函式限制在歐幾里德單位球體上,並將其視為Sn-1的函式。 均勻性屬性表明,這個限制確定了如上定義的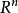 上的支撐函式。
上的支撐函式。
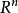
作為A的函式
擴展集合的支持函式與原始集合A密切相關:
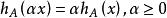
和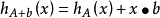
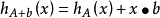
後者概括為
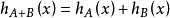
其中A + B表示閔可夫斯基總和:
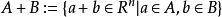
兩個非空緊湊凸集A和B的豪斯多夫距離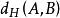 可以用支持函式來表示,
可以用支持函式來表示,
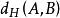
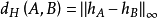
作為集合A的函式的支撐函式的屬性有時被總結為說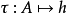 將非空緊湊凸集的集合映射到 在正均勻延伸為凸的球體上的所有實值連續函式的錐。 稍微濫用術語,
將非空緊湊凸集的集合映射到 在正均勻延伸為凸的球體上的所有實值連續函式的錐。 稍微濫用術語, 有時被稱為線性,因為它尊重閔可夫斯基加法,儘管它不是線上性空間上定義的,而是在非空緊湊凸集的(抽象)凸錐上。 映射
有時被稱為線性,因為它尊重閔可夫斯基加法,儘管它不是線上性空間上定義的,而是在非空緊湊凸集的(抽象)凸錐上。 映射 是具有豪斯多夫度量的錐體之間的等距,並且具有均勻範數的Sn-1上的連續函式族的子像素。
是具有豪斯多夫度量的錐體之間的等距,並且具有均勻範數的Sn-1上的連續函式族的子像素。