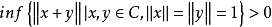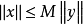對偶錐((dual cone)亦稱極錐,錐的極集。有時對偶錐也稱為負極錐,相應地也可定義正極錐。實線性空間的理論常可推廣到凸錐的情形,即通常的向量的線性組合概念可換為正線性組合概念。這時,對偶錐就起著對偶空間的作用。
基本介紹
- 中文名:對偶錐
- 外文名:dual cone
- 適用範圍:數理科學
定義,錐,立體錐,正則錐,正規錐,
定義
設𝟀是實線性空間,C⊂𝟀是凸錐,則𝟀上相對於C的負和零線性泛函的集合,即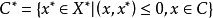 是實線性空間
是實線性空間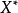 中的錐,稱
中的錐,稱 為C的對偶錐。由於將上述不等式中的0換為1仍得到相同的集合,因此亦稱
為C的對偶錐。由於將上述不等式中的0換為1仍得到相同的集合,因此亦稱 為C的對偶錐。有時對偶錐也稱為負極錐。類似地可以定義正極錐。
為C的對偶錐。有時對偶錐也稱為負極錐。類似地可以定義正極錐。
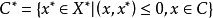
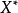


錐
[cone]
這裡所說的錐是定義在實線性空間上的。設C是實線性空間𝟀的子集,如果對任意x∈ C和λ>0都有λx∈ C成立,則稱C是一個錐。若0∈ C,則稱錐C為尖錐(pointed come)。如果A⊂𝟀,則稱包含A的最小錐為由A生成的錐,即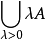 。如果𝟀中的錐C還是凸集,則稱C 是一個凸錐(convex cone)。由A(⊂𝟀)生成的凸錐即是A中元素所有正線性組合全體構成的集合。當凸錐C滿足C∩(-C)= {0} 時,則可以在𝟀上定義一個由C決定的半序關係。
。如果𝟀中的錐C還是凸集,則稱C 是一個凸錐(convex cone)。由A(⊂𝟀)生成的凸錐即是A中元素所有正線性組合全體構成的集合。當凸錐C滿足C∩(-C)= {0} 時,則可以在𝟀上定義一個由C決定的半序關係。
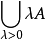
立體錐
[solid cone]
設𝟀是可分的局部凸線性空間,C 是𝟀中的尖錐,如果C不包含一維子空間,則稱C是突出的(salien)。如果C是𝟀中的內部非空的突出的尖凸錐,則稱C為立體錐。此時,X上相對於C的任意正線性泛函f,即對任意x∈C都有f(x)≥0成立,都是連續的。
正則錐
[regular cone]
設C是巴拿赫空間空間𝟀的空子集,如果C是𝟀作為實線性空間的突出的尖凸錐,則C可以在𝟀上定義半序關係。如果C中任意遞增且有序有界序列都收斂,則稱C是正則錐。如果C 中任意遞增且範數有界序列都收斂,則稱C 是完全正則錐(completely regularcone)。如果C是正則的和立體的,則C是完全正則的。
正規錐
[normal cone]
設C是巴拿赫空間𝟀的非空子集,如果C是𝟀作為實線性空間的突出的尖凸錐,∈ 是由C 所導出的半序關係。如果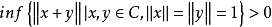 ,則稱C是正規的(normal)。此時,C是正規錐等價於範數的半單調(semimonotondicty):存在常教M>0,使得當0≤x≤y時都有
,則稱C是正規的(normal)。此時,C是正規錐等價於範數的半單調(semimonotondicty):存在常教M>0,使得當0≤x≤y時都有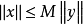 成立。
成立。