基本介紹
- 中文名:泛函
- 外文名:functional
- 性質:函式的函式
- 內容:從函式空間到數域的映射
- 常見泛函:線性泛函和二次型泛函
- 學科:數學
產生
定義
常見泛函


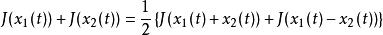

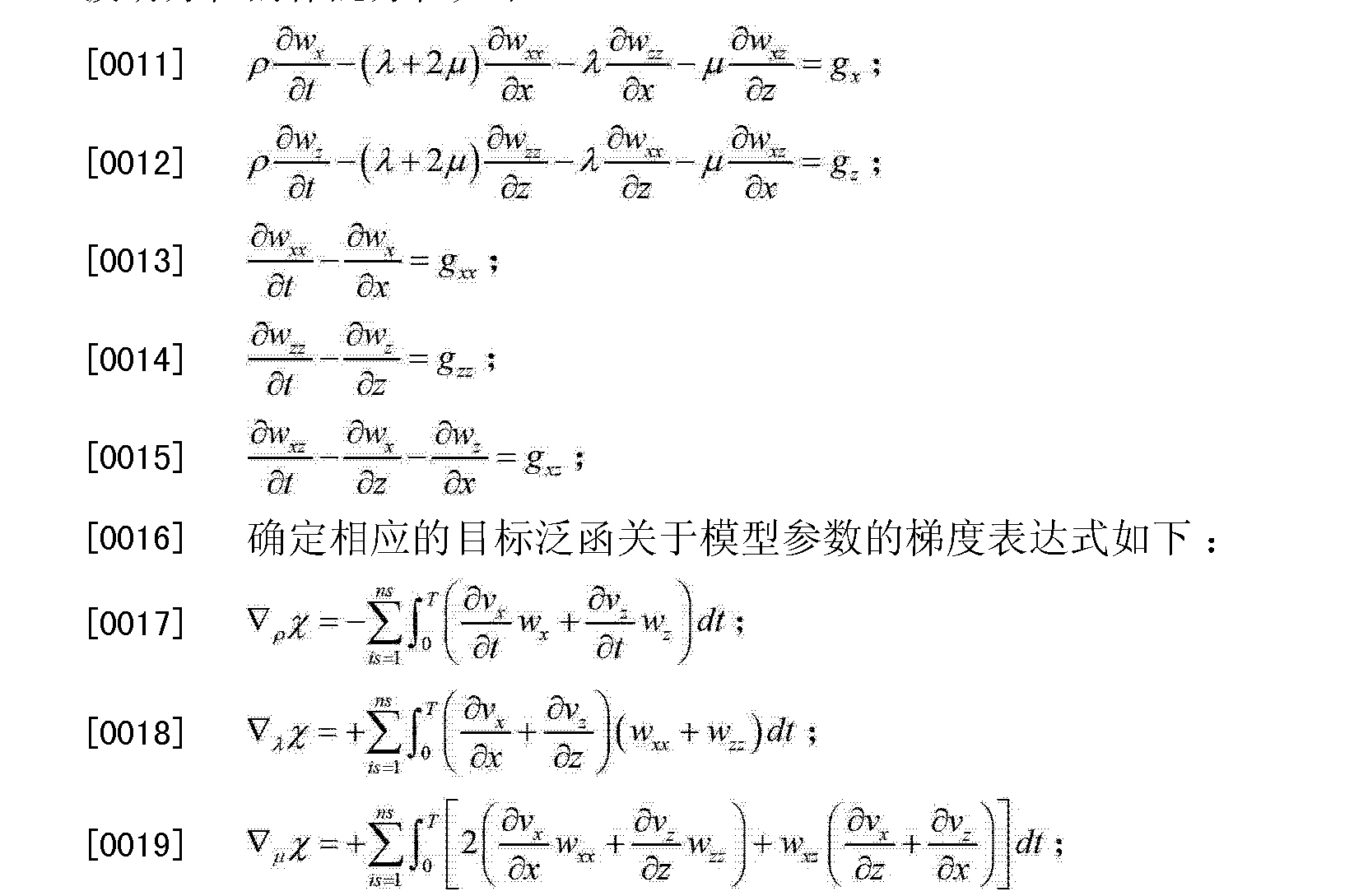


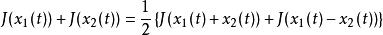

泛函是數學中重要的基本概念,是現代數學的重要研究對象之一,也是數學與其它領域研究與套用的一個重要工具。泛函分析是研究拓撲線性空間到拓撲線性空間之間滿足各種拓撲...
泛函分析是20世紀30年代形成的數學分科,是從變分問題,積分方程和理論物理的研究中發展起來的。它綜合運用函式論,幾何學,現代數學的觀點來研究無限維向量空間上的...
無限維分析學的一個新分支。它起源於量子物理學中的連續積分和機率論中的隨機過程的樣本空間的研究。泛函積分方法已深入到分理化量子場論、基本粒子理論、隨機力學...
通常的函式在 R或C(n是自然數)中的集合上定義。泛函數常在函式空間甚至抽象空間中的集合上定義,對集合中每個元素取對應值(實數或複數)。通俗地說,泛函數是以...
在數學和理論物理中,泛函導數(functional derivative)是向量導數的推廣。後者相對於一個有限維向量求導,而前者則相對於一個連續函式(可視為無窮維向量)求導。它們都...
泛函微分方程(functional differential equation)是帶有各種滯後量的微分方程(微分差分方程)、各種具有複雜變元的微分方程、帶有滯後量的積分微分方程等一類方程的概括和...
次可加泛函(sub-additive functional)是線性空間上的一類非負值函式。...... 次可加泛函(sub-additive functional)是線性空間上的一類非負值函式。中文名 次可加泛...
強制泛函是賦范線性空間中隨著範數的無限增大而一致趨向於無窮大的泛函。...... 強制泛函是賦范線性空間中隨著範數的無限增大而一致趨向於無窮大的泛函。...
本書自上世紀八十年代出版以來就在法國和世界很多國家被視為學習泛函分析和偏微分方程的主要教學用書,先後被翻譯成近十種文字。嚴謹、透徹、明晰地闡述了泛函分析的...
密度泛函理論 (英語:Density functional theory (DFT))是一種研究多電子體系電子結構的量子力學方法。密度泛函理論在物理和化學上都有廣泛的套用,特別是用來研究分子...
Gaussian 03 提供相當多的密度泛函理論(DFT) 75,76,448,449模型(DFT 方法和套用 的討論參見448, 450-461)。所有的DFT 模型都能計算能量78,解析梯度和真正的...
密度泛函理論(Density functional theory ,縮寫DFT)是一種研究多電子體系電子結構的量子力學方法。密度泛函理論在物理和化學上都有廣泛的套用,特別是用來研究分子和...
泛函分析基礎(科學出版社出版圖書)編輯 鎖定 作者:劉培德 ISBN:10位[7030163753] 13位[9787030163752] 出版社:科學出版社 出版日期:2006-01 定價:¥21.00 元...
電磁場的泛函法是指以泛函方程為電磁場問題數學模型的各種近似解法,區別於以函式方程為數學模型的各種經典的嚴格解法或近似解法。...
特徵泛函(characteristic functional)研究隨機過程分布律的重要分析工具。在經典機率論中,富氏分析方法,或者說得更具體一點,特徵函式方法是非常重要的。在研究抽象空間...
弱下半連續泛函(weakly lower semicontinuous functional)是指在巴拿赫空間中弱拓撲的意義下為下半連續的泛函。泛函,簡單上來說就是函式的函式,泛函就是定義域是一...
定義:設函式f(x)的定義域為R.若存在與x無關的正常數M,使 |f(X) |≤M|x|對一切實數x均成立,則稱f(x)為有界泛函. 舉例 f(x)=(sinx+cosx)x ...
莫爾斯泛函(Morse functional)是一種特殊泛函,是指所有臨界點為非退化的泛函。...... 莫爾斯泛函(Morse functional)是一種特殊泛函,是指所有臨界點為非退化的泛函。...
在數學和理論物理中,泛函導數是方嚮導數的推廣。後者對一個有限維向量求微分,而前者則對一個連續函式(可視為無窮維向量)求微分。它們都可以認為是簡單的一元微...
《線性泛函分析》是清華大學出版社2005年出版圖書。...... 本書以較小的篇幅介紹了線性泛函分析的基本內容:賦范空間和Banach空間,內積空間和Hilbert空間,線性運算元,緊...
《套用泛函分析》是2008年機械出版社出版的圖書,作者是程曹宗。...... 線性賦范空間和內積空間;第3章介紹線性運算元與線性泛函;第4章介紹有界線性運算元的譜與緊運算元;...
道格拉斯泛函是道格拉斯(Douglas,J.)為解決極小曲面問題引進的一個泛函。...... 道格拉斯泛函是道格拉斯(Douglas,J.)為解決極小曲面問題引進的一個泛函。...
閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。...... 閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。...
範數(norm)是數學中的一種基本概念。在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次性;③三角不等式。它常常被用來度量某個向量...
變分法是17世紀末發展起來的一門數學分支,是處理函式的數學領域,和處理數的函式的普通微積分相對。它最終尋求的是極值函式:它們使得泛函取得極大或極小值。變分...
