基本介紹
- 中文名:泛函微分方程
- 外文名:functional differential equation
- 所屬學科:數學
- 所屬問題:常微分方程(泛函微分方程)
- 別名:微分差分方程、時滯微分方程
- 相關概念:時滯,常微分方程等
- 相關人物:歐拉、克拉索夫斯基、加藤敏夫等
基本介紹
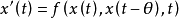
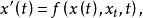


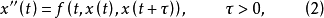
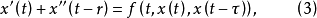

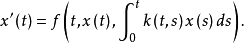

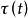
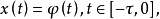
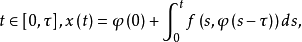
泛函微分方程的發展
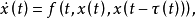
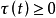
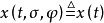
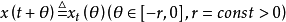
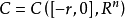
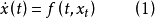
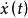

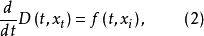
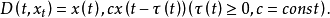
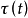
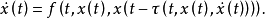

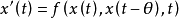
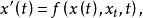


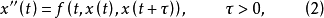
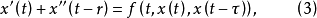

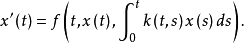

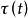
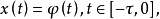
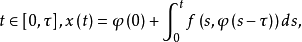
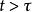
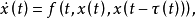
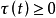
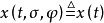
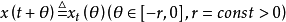
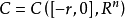
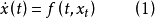
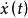

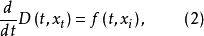
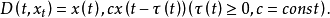
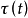
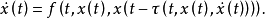
泛函微分方程(functional differential equation)是帶有各種滯後量的微分方程(微分差分方程)、各種具有複雜變元的微分方程、帶有滯後量的積分微分方程等一類方程的概括和...
線性泛函微分方程(linear functional differen-tial equation)是最重要的一類泛函微分方程,其中自治線性系統又是最基本的部分。線性系統理論涉及解的指數估計,通解的...
中立型泛函微分方程(neutral functional dif-ferential equation)最高階導數存在滯後的一類泛函微分方程。...
滯後型泛函微分方程(retarded functional dif-ferential equation)最基本的一類泛函微分方程,即概括各類時滯微分系統的一類泛函微分方程,是泛函微分方程理論的主體...
《剛性常微分方程及剛性泛函微分方程數值分析》是2010年湘潭大學出版社出版的圖書,作者是李壽佛。...
《泛函微分方程的相空間理論及套用》是2009年科學出版社出版的圖書,作者是王克,范猛。...
設t是微分方程的自變元,若方程的未知函式中出現不同於t但依賴於t的變元,則稱它為具有偏差變元的微分方程。...
《函式方程與微分方程的解析題》系統論述了函式方程與微分方程解析解的存在性問題,書中既有關於不含偏差變元函式方程與微分方程解析解存在性的經典工作的回顧,又...
常微分方程穩定性理論亦稱運動穩定性理論,是常微分方程理論的一個分支,其研究常微分方程的解在微小擾動下的性質。...
李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。克拉索夫斯基於1959年提出了在空間C中解釋軌線的觀點,同時引入李亞普諾夫泛函V(t,φ)的概念...
形式伴隨方程是在Rn中為確定常數變易公式的積分核而導出的相關方程。形式伴隨方程具體內容 設線性泛函微分方程ẋ(t)=L(t,xt)或 的解整體存在,ẋ(t)=L(t...
更新方程是一類特殊的泛函微分方程,在生態系統中用斯蒂爾傑斯積分表示的滯後型泛函微分方程稱為更新方程。...
《微分方程建模與分析》共三部分。第一部分首先介紹了一些預備知識,包括常微分方程的基本理論(如穩定性理論與分支理論)及敏感性與不確定性分析;然後詳細介紹了兩類...
《非線性微分方程》是2011年科學出版社出版的圖書,作者是傅希林、范進軍。本書系統地闡述了非線性常微分方程的基本理論、幾何理論、穩定性理論、振動理論與分支理論...
超球微分方程(hyperspherical equation)是數學物理中常見的常微分方程之一。連帶勒讓德方程經因變數變換後,可以得到超球微分方程;勒讓德方程和格根鮑爾方程都是它...
圖書信息作 者:郭大鈞 ISBN:7-5331-0491-7 出版社:山東科學技術出版社 出版時間:2002.10 版次: 字數: 頁數: 開本:32內容提要Banach空間中的常微分方程理論是...
求常微分方程滿足給定邊界條件的解的問題。亦即,設常微分方程為 \n\n\n對區間I上的點α1,α2,…,αk及值y(αi),y┡(αi),…,y(n-1)(αi)(i=1...
《右端不連續微分方程理論與套用》是2011年6月1日科學出版社出版的圖書,作者是黃立宏、郭振遠、王佳伏。1...
2、研究生:《常微分方程補充教程》、《微分方程邊值問題》、《微分方程幾何理論》、《泛函微分方程》和《非線性泛函分析》魯世平研究方向 編輯 ...
(2) 非線性剛性Volterra泛函微分方程Runge-Kutta法及一般多值方法的B-穩定與B-收斂理論。(3) 非線性剛性Volterra泛函微分方程Runge-Kutta法的收縮性及漸近穩定性...
唐先華,男,1963年3月出生,中南大學教授,主要從事泛函微分方程及離散動力系統方向的研究。...
黎永錦,男,1964年10月生於廣東省汕尾,現為中山大學數學系教授。92年研究生畢業於哈爾濱工業大學數學系,獲理學博士學位。研究興趣為:泛函分析,泛函微分方程等。已在...
常數變易公式是常微分方程的常數變易法線上性泛函微分方程的推廣。在拉普拉斯變換表示之下,由通解同樣可以得出常數變易公式。...
高國柱,1946年3月出生。套用數學學科教授。主要研究成果有“中立型泛函微分方程的穩定性”“周期解存在性及零點估計”等。發表“Stability Theorem for a Class of...
