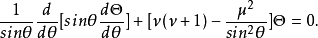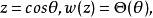超球微分方程(hyperspherical equation)是數學物理中常見的常微分方程之一。連帶勒讓德方程經因變數變換後,可以得到超球微分方程;勒讓德方程和格根鮑爾方程都是它的特殊情形。
基本介紹
- 外文名:hyperspherical equation
- 領域:數學
- 學科:數學物理
- 性質:常微分方程
- 推廣:勒讓德方程和格根鮑爾方程
概念,數學物理,常微分方程,連帶勒讓德方程,
概念
超球微分方程(hyperspherical equation)是數學物理中常見的常微分方程之一。形式為:
數學物理
以研究物理問題為目標的數學理論和數學方法。它探討物理現象的數學模型,即尋求物理現象的數學描述,並對模型已確立的物理問題研究其數學解法,然後根據解答來詮釋和預見物理現象,或者根據物理事實來修正原有的模型。
最早的物理問題研究就與數學息息相關。公元前6世紀古希臘畢達哥拉斯學派用整數之比論述琴弦的振動,發展起一套音樂理論。公元前3世紀阿基米德使用嚴格的幾何方法論證力學原理,求出若干平面圖形的重心。他還套用浮力定律研究旋轉拋物體在流體中的穩定性,套用槓桿原理得到許多幾何圖形的面積。公元2世紀托勒密利用三角方法研究光學。這些都是數學物理的早期例子。
文藝復興以後,數學物理有了長足發展。17世紀初義大利科學家伽利略建立了落體運動的正確定律;德國科學家克卜勒發現行星運動三大定律;1666年牛頓建立起萬有引力定律,1686—1687年完成巨著《自然哲學的數學原理》,以牛頓運動三定律為基礎建立起牛頓力學體系。其中的三體問題和各種經典的動力系統都是數學物理長期研究的對象。
微積分的發明為解決各種物理和力學問題提供了有力工具。對三體問題、擺的運動及彈性理論等問題的數學刻畫引導出一系列常微分方程,求解這些方程就成為牛頓力學中的重要數學問題。到18世紀,對弦振動問題、電磁場理論、流體力學和熱傳導等問題的深入研究開始了偏微分方程和偏微分方程組的研究,後人將這些偏微分方程以及具有物理意義的積分方程、微分積分方程和常微分方程統稱為數學物理方程。從17世紀末開始,對最速降線問題、等周問題的討論引發了變分法的創立。到18世紀中期,牛頓力學的基礎開始由變分原理刻畫,此後許多物理理論都以變分原理作為自己的基礎。
19世紀末由動力系統內行星和衛星軌道的穩定性問題導致微分方程定性理論的發展,到20世紀初,數學物理方程成為數學物理的主要內容。此後,等離子物理、固體物理、非線性光學、空間技術、核技術等方面不斷提出新的偏微分方程問題,使數學物理方程的內容進一步豐富起來,同時對這些方程的研究也促進了複變函數論、積分變換、特殊函式、變分法、調和分析、泛函分析乃至微分幾何學、代數幾何學、拓撲學等數學分支的發展。
20世紀初,對電磁理論和引力場的研究,使閔科夫斯基空間和黎曼空間的幾何大大發展,成為愛因斯坦狹義相對論和廣義相對論的基礎。許多物理量以向量、張量和旋量作為表達式。20世紀20年代量子力學的誕生依賴於希爾伯特空間理論,並套用了運算元的譜理論,量子力學發展成為量子場論時,再次套用了泛函分析的新工具,即20世紀30年代由匈牙利—美國數學家馮·諾伊曼發展起來的運算元代數理論。20世紀40—50年代核結構和基本粒子理論興起時,另一位匈牙利一美國數學家威格納開創的群表示論又成為主要工具。這些理論在數學的其他分支也起著重要作用。
近幾十年來,對基本粒子的內在對稱性研究導致了楊振寧—米爾斯理論(即規範場理論)的產生,並推動了纖維叢理論的發展;對經典統計物理學的研究促進了統計理論的深入研究;套用電子計算機後又發展起計算力學、計算物理等學科。數學物理內容日益豐富,同時又促進了數學的發展,成為產生數學新思想、新問題及新方法的一個源泉。數學物理中的許多方法和結果對數學在其他學科中的套用起了借鑑作用,推動了諸學科的發展。
常微分方程
分析數學的重要分支之一。包括一個自變數和它的未知函式以及未知函式的微商的等式叫做常微分方程。常微分方程研究的內容包括解的基本性質(如存在性、唯一性等),解的解析表達式或近似的解析表達式,解的定性性質(如運動穩定性、周期解的存在性等)以及解的數值解法。
常微分方程的發展歷史大體可分為四個階段:18世紀及其以前;19世紀初期和中期;19世紀末期及20世紀初期;20世紀中期以後。
19世紀末和20世紀初是常微分方程發展的第三個階段,主要在以下三個方面有重大發展:首先是關於常微分方程的解析理論的研究(見常微分方程解析理論),其次是常微分方程實域定性理論的創立(見常微分方程定性理論),第三是常微分方程攝動理論即小參數理論的建立。
從20世紀中期起,常微分方程的發展既深又廣,進入了一個新的階段,有以下幾方面的工作。
由於工程技術的需要而產生了新型問題和新的分支。例如工程控制論中火箭發動機的燃燒過程由於時滯現象而產生的帶有時滯的常微分方程(或稱微分差分方程),以及更廣義的泛函微分方程。又如由於空氣中的湍流對飛機運動的影響,使微分方程中帶有隨機攝動項,這類問題產生了隨機微分方程。
由於套用問題的需要而產生了一些近似的解析形式的解的求法。
電子計算機的出現與發展推動了常微分方程的研究,並取得一系列成果。起初,常微分方程由於解析解難求而轉向定性研究,當定性研究也困難時,又轉而用計算機“強攻”,得出一定的數值模擬結果後,反過來為定性研究提供了感性的新信息。這方面的研究正在興起。
常微分方程理論本身向高維數、抽象化的方向發展。例如從普通空間常微分方程向抽象空間常微分方程發展,從具體動力系統向抽象動力系統的發展,從實域定性理論向復域定性理論的發展等等。
連帶勒讓德方程
數學物理中常見的常微分方程之一。其形式為: