李亞普諾夫泛函方法

李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。克拉索夫斯基於1959年提出了在空間C中解釋軌線的觀點，同時引入李亞普諾夫泛函V(t,φ)的概念。

基本介紹

• 中文名：李亞普諾夫泛函方法
• 外文名：method of Liapunov functionals
• 適用範圍：數理科學

簡介

李亞普諾夫泛函方法是李亞普諾夫第二方法對泛函微分方程的一種推廣。

背景

用李亞普諾夫函式V(t,x)研究RFDE(f):ẋ(t)=f(t,x₁)的穩定性，因為有了拉茲密辛條件而大大擴展了套用範圍，然而仍有很大的局限性，而且無法證明V函式的存在性定理。正是由於這個原因，克拉索夫斯基於1959年提出了在空間C中解釋軌線的觀點，同時引入李亞普諾夫泛函V(t,φ)的概念。

具體內容

設泛函V:R×C→R連續，x(t,σ,φ)是方程過(σ,φ)的解，定義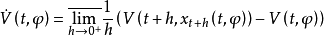

為V關於方程的全導數，或者說沿方程的解取上右導數。作為例子，觀察一個穩定性定理：設f:R×C→Rⁿ，使R×（C的有界子集）映入Rⁿ的有界集。u,v,w:R₊→R₊是連續的非減函式，u(s)，v(s)當s>0時取正值，且 u(0)=v(0)=0。若存在R×C到R上的連續泛函V，使得

則RFDE(f)的零解是一致穩定的。

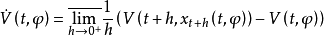
若s→∞時，u(s)→∞，則零解是一致有界的。若→∞時，w(s)>0，則零解是一致漸近穩定的。

套用

除了穩定性理論以外，V泛函還用於研究解的有界性，周期解與概周期解的存在性等問題。

對運算元型中立型泛函微分方程NFDE(D,f)，有一系列與RFDE(f)平行的套用結果。