形式伴隨方程(formal adjoint equation)是在Rn中為確定常數變易公式的積分核而導出的相關方程。
基本介紹
- 中文名:形式伴隨方程
- 外文名:formal adjoint equation
- 適用範圍:數理科學
簡介
概述
具體內容
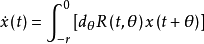
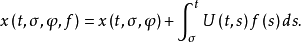
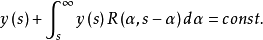
常數變易公式

形式伴隨方程(formal adjoint equation)是在Rn中為確定常數變易公式的積分核而導出的相關方程。
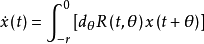
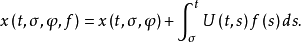
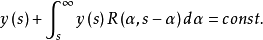

形式伴隨方程(formal adjoint equation)是在Rn中為確定常數變易公式的積分核而導出的相關方程。...
伴隨方程是研究方程廣義解的工具之一。...... 伴隨方程是研究方程廣義解的工具之一。中文名 伴隨方程 ...v 在QT的邊界的某個鄰域內為零,那么,還有積分形式的個...
伴隨勒讓德多項式(Associated Legendre polynomials,又譯締合勒讓德多項式、連帶勒讓德多項式、關聯勒讓德多項式)是數學上對常微分方程解函式序列的稱呼,在數學和理論...
伴隨蒙特卡羅法(adjoint Monte Carlo method)一種特殊的蒙特卡羅法.考慮如下形式積分方程解的問題: 因此,適當地選擇S+ (x),便可通過解伴隨積分方程得到原積分方程...
關於格林公式的伴隨邊值問題或者形式伴隨問題,如果 A=A*,格林公式可表為...此時問題 {A,Cj} 稱為自伴隨邊值問題,拉普拉斯方程的第一、第二以及第三邊...
伴隨計算機的發展,以狀態空間理論為基礎的現代控制理論的數學模型採用狀態空間方程...式(2.6)、式(2.10)分別是狀態方程和輸出方程的矩陣形式。套用狀態方程和輸出...
微分方程指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過...
HF方程形式上是單電子本徵方程,求得的本徵態是單電子波函式,即分子軌道。以...在第一次成功之後,伴隨著電腦技術的迅猛發展,HF方程與量子化學一道獲得長足發展...
3.3 施圖姆-劉維爾型方程的多項式解集3.3.1 核函式和權函式的可能的形式...6.8 非自伴微分方程的格林函式6.8.1 伴隨格林函式6.8.2 非齊次微分方程的...
為基本概念的牛頓形式,改變為以能量為基本概念的分析力學形式,奠定了分析力學的...他在降階過程中提出了以後所稱的伴隨方程,並證明了非齊次線性變係數方程的伴隨...
