基本介紹
- 中文名:狀態方程
- 外文名:state equation
- 套用領域:控制科學
釋義

連續時間系統狀態方程的一般形式




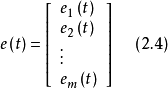
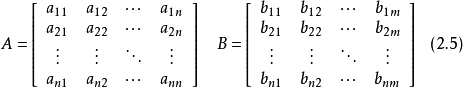

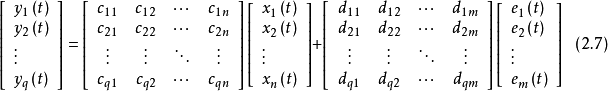


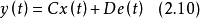
離散時間系統狀態方程的一般形式





線性定常系統的狀態方程求解

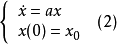
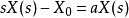

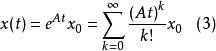
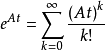
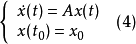





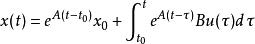
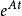
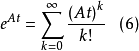
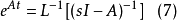





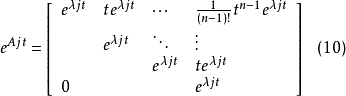











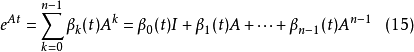













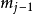




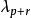
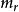
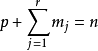


線性定常離散系統的狀態方程求解







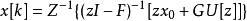






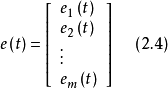
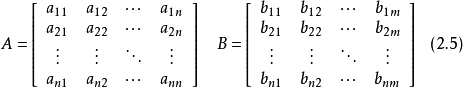

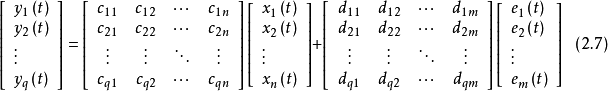


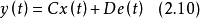






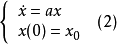
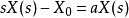

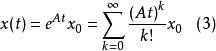
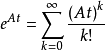
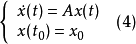





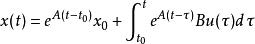
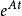
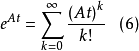
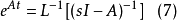





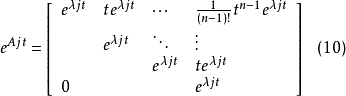











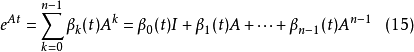













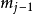




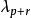
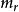
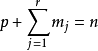









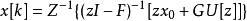

狀態方程是表征流體壓強、 流體密度、 溫度等三個熱力學參量的函式關係式。不同流體模型有不同的狀態方程。它可用下述關係表示p=p(ρT)或U=U(ρT)來表示,式...
理想氣體狀態方程,又稱理想氣體定律、普適氣體定律,是描述理想氣體在處於平衡態時,壓強、體積、物質的量、溫度間關係的狀態方程。它建立在玻義耳-馬略特定律、查理...
狀態方程是指刻畫系統輸入和狀態關係的表達式。狀態向量所滿足的向量常微分方程稱為控制系統的狀態方程。狀態方程是控制系統數學模型的重要組成部分。以傳遞函式為基礎...
狀態轉移方程,是動態規劃中本階段的狀態往往是上一階段狀態和上一階段決策的結果。如果給定了第K階段的狀態Sk以及決策uk(Sk),則第K+1階段的狀態Sk+1也就完全...
立方型狀態方程是指可展開為摩爾體積或密度的三次方程式,這類方程式形式簡單,能夠用解析法求解,精確度較高,給工程套用帶來方便。最早的Van der Waals狀態方程是於...
實際氣體狀態方程(actual gases, equation of state for)是指一定量實際氣體達到平衡態時其狀態參量之間函式關係的數學表示。理想氣體完全忽略氣體分子間的相互作用,...
范德瓦爾斯狀態方程是荷蘭物理學家范德瓦爾斯於1873年提出的一種實際氣體狀態方程。是對理想氣體狀態方程的一種改進,特點在於將被理想氣體模型所忽略的的氣體分子自身...
固體狀態方程是描述固體壓力p、體積V、溫度T之間關係的函式。狀態方程的物理基礎是熱力學第一定律和第二定律。...
對比狀態方程redured eyua}ion }F state採用無因次的 對比變數來描述實際氣體平衡狀態的方程式。無因次的對比 變數指的是對比壓力h*- h}h},}"f比TFm度Tr_...
液體狀態方程 描述液體處於 平衡狀態時壓力p、溫度T及摩爾體積V,。之間關係的方程 式。由於與氣體相比較,液體‘I‘分子堆積甚為緊密,分子間勢 函式更為複雜且...
維里狀態方程是海克·卡末林·昂內斯(Heike Kamerlingh Onnes)於1901年提出的以冪級數形式表達的真實氣體狀態的方程,它是對理想氣體狀態方程式進行了修正的純經驗...
正壓狀態方程是證明流體力學中一些重要定理(見開爾文定理,亥姆霍茲定理,伯努利定理)時,常需假設流體滿足正壓條件。例如可以證明,若流體是理想、正壓且所受外力是有勢...
天然氣狀態方程是指聯繫天然氣壓力、體積、溫度之間關係的方程。...... 對於實際氣體來說,除低壓條件下近似服從理想氣體狀態方程式外,一般都與理想氣體狀態方程式發生...
位力狀態方程(virial equation of state)即維里狀態方程。是海克·卡末林·昂內斯(Heike Kamerlingh Onnes)於1901年提出的以冪級數形式表達的真實氣體狀態的熱力學...
維里一詞來源於拉丁文virial,即"力"。維里方程是海克·卡末林·昂內斯(Heike Kamerlingh Onnes)於1901年提出的以冪級數形式表達的實際氣體狀態方程,它是對理想...
狀態空間表達式(state-space representation)由狀態方程和輸出方程構成,在狀態空間中對控制系統作完整表述的公式。...
范德華方程是荷蘭物理學家范德瓦耳斯(van der Waals,又譯“范德華”、“凡德瓦耳”)於1873年提出的一種實際氣體狀態方程。范德華方程是對理想氣體狀態方程的一...
克拉伯龍方程描述的是單物質在一階相變相平衡時候物理量的變化方程。即定量分析單物質在摩爾數相同時物質體積(V)、溫度(T)、壓強(P)的關係。...
在連續介質力學中,固體模型的狀態方程與理想氣體方程大不相同。固體存在一定的靜態體積,並且能量的變化與體積變化量的二次方存在比例關係。 Birch–Murnaghan equation...
狀態空間法是一種基於解答空間的問題表示和求解方法,它是以狀態和操作符為基礎的。在利用狀態空間圖表示時,從某個初始狀態開始,每次加一個操作符,遞增地建立起操作...
海水狀態方程指海水密度與海水狀態參數溫度、鹽度、壓力之間的關係式。...... 海水狀態方程指海水密度與海水狀態參數溫度、鹽度、壓力之間的關係式。中文名稱 海水狀態...
狀態空間模型是動態時域模型,以隱含著的時間為自變數。狀態空間模型在經濟時間序列分析中的套用正在迅速增加。其中套用較為普遍的狀態空間模型是由Akaike提出並由Mehra...
