基本介紹
簡介
方程形式



氣體種類 | a [kPa 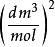 | b [  |
氦氣(He) | 3.45 | 0.024 |
氫氣(H2) | 24.32 | 0.027 |
氮氣(N2) | 141.86 | 0.039 |
氧氣(O2) | 137.80 | 0.032 |
二氧化碳(CO2) | 364.77 | 0.043 |
水蒸氣(H2O) | 557.29 | 0.031 |




氣體種類 | a [kPa 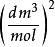 | b [  |
氦氣(He) | 3.45 | 0.024 |
氫氣(H2) | 24.32 | 0.027 |
氮氣(N2) | 141.86 | 0.039 |
氧氣(O2) | 137.80 | 0.032 |
二氧化碳(CO2) | 364.77 | 0.043 |
水蒸氣(H2O) | 557.29 | 0.031 |
范德華方程是荷蘭物理學家范德瓦耳斯(van der Waals,又譯“范德華”、“凡德瓦耳”)於1873年提出的一種實際氣體狀態方程。范德華方程是對理想氣體狀態方程的一...
范德瓦爾斯方程(又譯范德華方程),簡稱范氏方程,是荷蘭物理學家范德瓦爾斯於1873年提出的一種實際氣體狀態方程。范氏方程是對理想氣體狀態方程的一種改進,特點在於...
約翰尼斯·迪德里克·范·德·瓦耳斯(通常稱為范德·瓦耳斯或范德華,Johannes Diderik van der Waals,1837年-1923年),荷蘭物理學家。曾任阿姆斯特丹大學教授。對...
雷德利希-鄺氏狀態方程(Redlich-Kwong equation of state),簡稱R-K方程,是物理化學中基於范德瓦耳斯方程的一個近似描述真實氣體行為的狀態方程。此方程是由猶太裔...
天然氣狀態方程范德華方程式 編輯 對於實際氣體來說,除低壓條件下近似服從理想氣體狀態方程式外,一般都與理想氣體狀態方程式發生偏差,有時甚至發生較大的偏差。...
范德華方程(van der Waals equation)(一譯范德瓦耳斯方程),簡稱范氏方程,是荷蘭物理學家范德華於1873年提出的一種實際氣體狀態方程。范氏方程是對理想氣體狀態...
方程 ; 第三種方法Lilienfeld 等人提出的基於改造贗勢的方法 ; 第四種方法是構造新的范德 華密 度泛函的方法 , 其中以 Dion 等人 [16] 提出的 vdW-DF 泛函...
1.3.2 范德華方程習題2 化學反應熱量計算3 化學反應進行的方向和判據4 化學平衡5 溶液6 相平衡第2篇 冶金反應動力學7 冶金反應過程的動力學...
3.6 實際氣體狀態方程3.6.1 維里方程3.6.2 范德華方程3.6.3 R—K方程3.7 對應態原理與通用壓縮因子圖3.7.1 范德華對應態方程...
高壓或低溫氣體的狀態變化就較顯著地偏離氣態方程,對方程需要按實際情況加以修正。修正的方法很多,過去常用的一種修正方程叫做范德華方程。它是以考慮分子間的相互...
9.2.3克拉珀龍?克勞修斯方程(Clapeyron?Clausius equation)1519.3實際氣體狀態方程(equation of state)1529.3.1范德華方程(Van der Waals equation)152...
1.3 真實氣體狀態方程1.3.1 真實氣體對理想氣體的偏差1.3.2 范德華方程1.3.3 維里方程1.3.4 其他重要方程1.3.5 普遍化的真實氣體狀態方程與壓縮因子...
代表範例 范德華方程 問題來源 世界之初,是“先有雞”還是“先有蛋”這一個讓人百思不得其解的古老爭論謎題,先有雞先有蛋讓人們總是不斷地去探索並討論生...
1.3實際氣體狀態方程1.3.1實際氣體的行為1.3.2范德華方程1.4氣體的液化和物質的臨界狀態1.4.1氣體的液化1.4.2氣體的臨界狀態1.4.3對應狀態原理...
1.5 范德華方程 1.6 普遍化計算和對應狀態原理 1.7 維里方程 Ⅱ. 物質的熱性質 1.8 熱力學第一定律 1.9 標準熱容 1.10 標準相變焓 1.11 標準生成焓和標準...
2.5.2范德華方程………(60)2.5.3 BWR方程………...11.7.3燃氣引射混合器的基本方程………(356)11.7.4燃氣引射混合器的供氣壓力極限與囗效率………(357...
雖然體積為三次冪的狀態方程,如范德華方程和Redlich-Kwong方程等也能定性地描述液體的P、V、T行為,但一般來說,不能定量地計算遠離臨界態和具有較高的對比密度的...
▪ 反應速率 ▪ 范德華方程 ▪ 芳香性 ▪ 芳香族化合物 ▪ 放射性 ▪ 非金屬 ▪ 非晶體 ▪ 非均相催化劑 ▪ 菲舍爾投影式 ▪ 費林試...
1.3.2范德華方程71.3.3維里(Virial)方程81.3.4貝賽羅(Berthelot)方程91.3.5R.K(Redlich·Kwong)方程91.3.6馬丁·侯(Martin·侯虞均)方程9...
二、理想氣體狀態方程4三、摩爾氣體常數R的求取5四、分壓定律和分體積定律6五、氣體分子運動論7第二節實際氣體8一、壓縮因子8二、范德華方程8...
1 4真實氣體狀態方程201 4 1范德華方程201 4 2維里方程231 4 3其它的真實氣體狀態方程舉例241 5壓縮因子和普遍化壓縮因子圖24...
