范德瓦爾斯方程
式中
a 為度量分子間引力的參數
b 為每個分子平均占有的空間大小(即氣體的體積除以總分子數量)
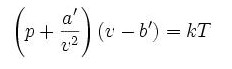 范德瓦爾斯方程
范德瓦爾斯方程T 為熱力學溫度
R 為普適氣體常數
m 為氣體質量
M 為摩爾質量
在第二個方程里,氣體物質的量為 1mol
v 為體積
范德瓦爾斯常量
下表列出了部分氣體的a,b 的值
氣體 | a / (atm·L^2/mol^2) | b / (L/mol) |
氫 | 0.191 | 0.0218 |
氧 | 1.360 | 0.03183 |
氮 | 1.390 | 0.03913 |
氯 | 6.493 | 0.05622 |
氦
| 0.03412 | 0.02370 |
氖
| 0.2107 | 0.01709 |
汞蒸氣 | 8.093 | 0.01696 |
二氧化碳 | 3.592 | 0.04267 |
水蒸氣 | 5.464 | 0.03049 |
適用範圍
范氏方程對氣-液臨界溫度以上流體性質的描寫優於理想氣體方程。對溫度稍低於臨界溫度的液體和低壓氣體也有較合理的描述。
但是,當描述對象處於狀態參量空間(P,V,T)中氣液相變區(即正在發生氣液轉變)時,對於固定的溫度,氣相的壓強恆為所在溫度下的飽和蒸氣壓,即不再隨體積V(嚴格地說應該是單位質量氣體占用的體積,即比容)變化而變化,所以這種情況下范氏方程不再適用。
方程提出
水分子之間的范氏引力(中國大陸的中學教科書稱為“范德瓦爾斯力”或“范德華力”)
一個雙原子分子的排斥體積(圖中黑色的部分)下面以理想氣體狀態方程為基礎,推導范氏方程。若把氣體視為由體積無限小、相互之間無作用力的分子組成,這種模型便是理想氣體模型,與其相對應的狀態方程是:
若拋棄前一個的假設,把組成氣體的分子視為有一定大小的剛性球(其半徑稱為范德瓦爾斯半徑),用b 表示這些“球”的體積,上面的方程便改寫為:
在這裡,每個分子的“占有體積”v 被所謂“排斥體積”v - b 代替,反映了分子在空間中不能重疊。若氣體被壓縮至體積接近分子體積之和(即分子間空隙v - b 趨向於0),那么其壓強將趨於無窮大。
下一步,我們考慮原子對之間的引力。引力的存在會使分子的平均亥姆霍茲自由能下降,減少量正比於流體的密度。但壓強的大小滿足熱力學關係
式中A* 為每個分子的亥姆霍茲自由能。由此得到,引力使壓強減小的量正比於1/v²。記該比例常數為a,可得
這便是范氏方程。
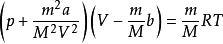
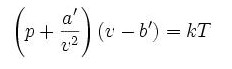 范德瓦爾斯方程
范德瓦爾斯方程
