J.D 范德瓦爾斯

J.D 范德瓦爾斯（Johannes Diderik van der Waals），1837年11月23日生於荷蘭的萊頓，父親名叫雅各布.范德瓦爾斯，母親名叫伊莉莎白·范登伯格（Elisabeth van den Burg）。范德瓦爾斯在家鄉結束了初等教育後，成為一名中學教員。雖然他因不懂古典語言而未能參加大學人學考試，但在1862—1865年期間，他利用業餘時間在萊頓大學繼續學習，並獲得了數學和物理學的教師證書。

基本介紹

• 中文名：J.D 范德瓦爾斯
• 外文名：Johannes Diderik van der Waals
• 出生地：荷蘭萊頓
• 出生日期：1837年11月23日

個人簡介

1864年，范德瓦爾斯任德文特一所中學的教師。1866年到海牙，先當該城一所中學的教師，後任該校校長。新的立法取消了理工科大學生人學前必須受古典語言教育的規定，使范德瓦爾斯能夠參加大學考試。1876年頒布了新的高等教育法，將阿姆斯特丹古老的雅典語學院擴充成綜合大學，范德瓦爾斯被任命為該校第一名物理學教授。他和同事范托夫（Van‘ t Hoff）、遺傳學家休戈·德弗里斯（Hugo de vries）使該校聲譽大增。儘管各處向他發出盛情的邀請，但他一直忠實地留在該校，直到退休。范德瓦爾斯對他論文的課題發生興趣的直接原因，是克勞修斯的論文中將熱看成是一種運動現象，使他想對安德魯斯1869年證明氣體存在臨界溫度時所作的實驗尋找一種解釋。范德瓦爾斯天才地發現，必須考慮分子的體積和分子間的作用力（現在一般稱為范德瓦爾斯力），“才能建立氣體和液體的壓強、體積、溫度之間的關係。1864年，范德瓦爾斯同A．M。斯密特（Anna Magdalena Smit）結婚。妻子早亡，他沒有再結婚。他們有三個女兒和一個兒子。女兒瑪黛萊茵在母親去世後料理家務，照顧父親；伊利莎白是歷史教員和著名詩人；迪代莉卡是英語教師。兒子迪代里克（Johannes Diderik Jr．）在1903—1908年間擔任格羅寧根大學物理學教授，後來繼承父親的職務，在阿姆斯特丹大學主持物理學講座。范德瓦爾斯的主要愛好是散步和朗誦，特別是在鄉郊散步。1923年8月8日他在阿姆斯特丹逝世。

輝煌人生

1873年他以這篇論文取得了博士學位，使他立刻進入了第一流物理學家的行列。在這篇論文中，他提出了包括氣態和液態的“物態方程”，論證了氣液態混合物不僅以連續的方式互相轉化，而且事實上它們具有相同的本質。關於范德瓦爾斯第一篇論文中提出的這個結論的重要性，在J．C．麥克斯韋的一書中有這樣的評價：“毫無疑問，范德瓦爾斯的名字將很快出現在第一流的分子科學家的名單中”，“可以肯定，不止一個科學家正在注意學習他的論文所用的‘低地荷蘭語’”（麥克斯韋可能想說“低地德語”，但這是不對的，因為荷蘭語有權自成為一種語言）。後來，他就這個課題和與此有關的課題又寫了大量論文，發表在和上，並被譯成多種文字。范德瓦爾斯經過艱苦的努力，於1880年發表了第二項重大發現，當時他稱之為“對應態定律”。這個定律指出：如果壓強表示成臨界壓強的單調函式，體積表示成臨界體積的單調函式，溫度表示成臨界溫度的單調函式，、就可得到適用於所有物質的物態方程的普遍形式，因為在這個方程中，a，b，產這三個常數可用特殊物質的臨界值來表示，因此在方程中消失。正是由於在這個定律的指導下進行實驗，J．杜瓦才在1898年製成了液態氫，翁納斯在1908年製成了液態氦。翁納斯因研究低溫和製成液態氦而榮獲1913年的諾貝爾物理學獎。他在1910年寫道：“我們一直把范德瓦爾斯的研究看成是實驗取得成功的關鍵，萊頓的低溫實驗室是在他的理論影響下發展起來的。十年後，即18

90年，關於“二元溶液理論”的第一篇論文在《荷蘭年鑑》上刊出，這是范德瓦爾斯的又一項重大成就。他把物態方程和熱力學第二定律結合起來，創造了一種圖示法，以吉布斯在“非均勻物質的平衡”這篇論文中首次提出的形式用一個面表示他的數學公式。為紀念吉布斯，他把這個面稱為“w面”，因為吉布斯用希臘字母w作為自由能的符號，他認為自由能對平衡有著重大意義。二元混合物理論引起了一系列實驗，首先是庫恩的實驗。他發現，臨界現象的特徵完全可由理論預言。關於這個課題的報告後來收編人范德瓦爾斯和柯恩斯塔姆教授合著的>（熱力學教程）。還應當提到范德瓦爾斯關於毛細現象的熱力學理論，其基本形式是在1893年首次提出的。該理論認為，在液體和蒸氣之間的邊界層存在著密度的逐漸變化，儘管變化是很快的。這個觀點和吉布斯的不同，吉布斯假設從液體到蒸氣，密度是突變的。拉普拉斯早年建立了毛細現象的理論，范德瓦爾斯卻認為分子永遠在作高速運動。在臨界溫度附近所作的關於這個現象的實驗支持了范德瓦爾斯的觀點。 范德瓦爾斯獲得了許多榮譽，特別應提到的是；他是劍橋大學的榮譽博士，莫斯科帝國自然科學學會名譽會員，愛爾蘭皇家科學院名譽院士，美國哲學協會名譽會員，法國研究院通訊院士，柏林皇家科學院通訊院士，比利時皇家科學院名譽院士，倫敦化學協會外籍會員，美國國家科學院外籍院士，羅馬科學院外籍院士。

范德瓦爾斯方程

范德瓦耳斯方程（van der Waals equation），簡稱范氏方程，是荷蘭物理學家范德瓦耳斯於1873年提出的一種實際氣體狀態方程。范氏方程是對理想氣體狀態方程的一種改進，特點在於將被理想氣體模型所忽略的的氣體分子自身大小和分子之間的相互作用力考慮進來，以便更好地描述氣體的巨觀物理性質。范德瓦耳斯方程更常用的形式為 (N=摩爾數)

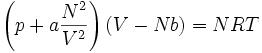
式中，p 為氣體的壓強；a' 為度量分子間引力的唯象參數；b' 為單個分子本身包含的體積；v 為每個分子平均占有的空間大小（即氣體的體積除以總分子數量）；k 為玻爾茲曼常數；T 絕對溫度。在第二個方程里，V 為總體積；a 為度量分子間引力的參數；b 為1摩爾分子本身包含的體積之和 b = NAb'；R 為普適氣體常數；NA 為阿伏加德羅常數.。在上述方程中必須嚴格區分總體平均性質和單個分子的性質。譬如，第一個方程中的v 是每個分子平均占有空間的大小（可以理解成分子平均“勢力範圍”的大小），而b' 則為單個分子本身“包含”的體積（若為單原子分子如稀有氣體，b '就是原子半徑內包含的體積）。范氏方程對氣-液臨界溫度以上流體性質的描寫優於理想氣體方程。對溫度稍低於臨界溫度的液體和低壓氣體也有較合理的描述。但是，當描述對象處於狀態參量空間(P,V,T)中氣液相變區（即正在發生氣液轉變）時，對於固定的溫度，氣相的壓強恆為所在溫度下的飽和蒸氣壓，即不再隨體積V（嚴格地說應該是單位質量氣體占用的體積，即比容）變化而變化，所以這種情況下范氏方程不再適用。

范德瓦爾斯半徑

范德瓦爾斯半徑曾稱范德華半徑。在液體和分子晶體中，分子間保持一定的接觸距離，即每個分子占有一定的體積。范德瓦爾斯半徑就是指相鄰分子相互接觸的原子表現出來的半徑。例如，Cl2晶體或其他含氯分子組成的晶體中，相鄰分子兩個相互接觸的兩個氯原子間的距離約為360皮米，它的一半就是氯原子的范德瓦爾斯半徑，180皮米。范德瓦爾斯半徑比原子共價半徑大，變動範圍也大，即守衡性差。鹵素X和O、S、Se、Te等原子的范德瓦爾斯半徑，分別和它們相應的一價負離子X-，二價負離子O2-、S2-、Se2-、Te2-的離子半徑大致相等。例如，C1的范德瓦爾斯半徑為180皮米，C1-的離子半徑為181皮米。氧元素的范德瓦爾斯半徑為140皮米，O2-的離子半徑也為140皮米。范德瓦爾斯半徑可從有關手冊中查找。

對應態原理

對應態原理又稱對比態原理，不同物質如果具有相同的對比壓力pr（壓力p與臨界壓力pc之比）和對比溫度Tr(溫度T與臨界溫度Tc之比)，就是處於對應態,這時它們的各種物理性質都具有簡單的對應關係。對應態原理是受臨界點時各種氣體的壓縮因子近似相等這一事實的啟示而發現的，也可套用統計力學原理從理論上導出。在p－V－T關係的計算中，根據對應態原理，可將實際氣體的具有兩個特徵參數的狀態方程（如范德瓦耳斯方程、RK方程、PR方程等），轉化為不含特徵參數的普遍化狀態方程，也可將壓縮因子和對比溫度、對比壓力的關係繪製成普遍化壓縮因子圖。利用普遍化狀態方程和普遍化壓縮因子圖，只需知道物質的臨界溫度和臨界壓力,就可作p－V－T關係的近似計算，因而對應態原理在工程設計中得到廣泛套用。而且流體的粘度、熱導率、分子擴散係數等物性參數，以及維里係數、逸度係數、焓、熱容等熱力學參數,也可以根據對應態原理估算，編繪出相應的普遍化圖表以供查考。

理想氣體狀態方程

理想氣體狀態方程（ideal gas，equation of state of），描述理想氣體狀態變化規律的方程。質量為M的理想氣體，其狀態參量壓強p、體積V和絕對溫度T之間的函式關係為：ρV=MRT/μ=νRT，式中μ和v分別是理想氣體的摩爾質量和摩爾數；R是氣體常量。對於混合理想氣體，其壓強p是各組成部分的分壓強p1、 p2、……之和，故pV=（ p1+ p2+……）V=(v1+v2+……)RT，式中v1、v2、……是各組成部分的摩爾數。以上兩式是理想氣體和混合理想氣體的狀態方程，可由理想氣體嚴格遵循的氣體實驗定律得出，也可根據理想氣體的微觀模型，由氣體動力學理論導出。在壓強為幾個大氣壓以下時，各種實際氣體近似遵循理想氣體狀態方程，壓強越低，符合越好，在壓強趨於零的極限下，嚴格遵循。

公式:pV=nRT，p為氣體壓強，單位Pa。V為氣體體積，單位m3。n為氣體的物質的量，單位mol，T為體系溫度，單位K。R為比例係數，數值不同狀況下有所不同，單位是J/（mol·K）

推導：經驗定律

（1）Boyle定律

當n，T一定時 V，p成反比，即V∝（1/p）①

（2）Charles---Gay·Lussac定律

當n，p一定時 V，T成正比，即V∝T ②

（3）Avogadro定律

當T，p一定時 V，n成正比，即V∝n ③

由①②③得

V∝（nT/p） ④

將④加上比例係數R得

V=（nRT）/p 即pV=nRT