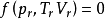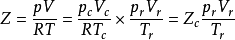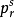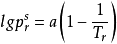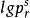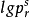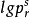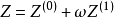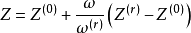對應態原理又稱對比態原理，不同物質如果具有相同的對比壓（壓力與臨界壓力之比）和對比溫度（溫度與臨界溫度之比），就是處於對應態，這時它們的各種物理性質都具有簡單的對應關係。對應態原理是受臨界點時各種氣體的壓縮因子近似相等這一事實的啟發而實現的。
基本介紹
- 中文名：對應態原理
- 外文名：Principle of corresponding states
- 別名：對比態原理
- 發現原因：臨界點各氣體壓縮因子近似相等
- 套用：計算流體混合物等
- 所屬學科：工程技術
基本定義,三參數對應態原理,以Zc作為第三參數的對應態原理,以ω作為第三參數的對應態原理,
基本定義
對比溫度Tr、對比壓力pr、對比摩爾體積Vr的定義為：
將對比參數的定義式代入Van der Waals方程得
由此可看出，不論是何種流體，只要它處在相同的Tr、Vr下，那么pr一定相同。對應態原理認為，在相同的對比狀態下，所有的物質表現出相同的性質。運用該原理研究氣體的p-T-V關係就可得到普遍化的真實氣體方程式。
該方程就是Van der Waals提出的兩參數對應態原理，式中沒有任何參數，成為對任何氣體都可適用的方程式；換言之，對於不同的氣體，當具有相同的對比溫度和對比壓力時，則具有相同的對比體積（或壓縮因子）。在數學上可表達為：
又因為
若式上式成立，必須要求臨界壓縮因子Zc是一固定常數，但大部分物質的Zc為0.2~0.3，並不是個常數。顯然，兩參數對應態原理只是一個近似的關係，只能適用於簡單的球形流體。
對應態原理是一種特別的狀態方程，也是預測流體性質最有效的方法之一。為了拓寬對應態原理的套用範圍和提高計算精度，研究者引入第三參數而建立的普遍化關係式。
三參數對應態原理
以Zc作為第三參數的對應態原理
LydersenL等以Zc作為第三參數，將壓縮因子表示為
即認為Zc相等的真實氣體，如果兩個對比參數相等，則第三個對比參數必相等。他們根據包括烴、醇、醚、酯、硫醇、有機鹵化物、部分無機物和水在內的82種不同物質的p-V-T性質和臨界性質數據，按Zc將所選物質分為0.23，0.25，0.27，0.29四組，分別得到了各組的Z和其他對比熱力學性質與Tr和pr的數據圖，不僅可用於氣相，還可用於液相。
以ω作為第三參數的對應態原理
除了以Zc作為第三參數外，還可以採用其他表示分子結構特性的參數作為第三參數，如Pitzer提出的偏心因子ω獲得了廣泛套用。
純態物質的偏心因子是根據物質的蒸氣壓定義的。實驗發現，純態流體對比飽和蒸氣壓
的對數與對比溫度Tr的倒數近似於直線關係，即滿足
實驗結果表明，不同的流體a的數值不同。但Pitzer發現，當將
對1/Tr作圖時，簡單流體（氬、氪、氙）的所有蒸氣壓數據都集中在同一直線上，而且該直線還通過Tr=0.7，
=-1這一點。然而其他流體（除H2、He外）在Tr=0.7時則有
<-1。考慮到一般流體與簡單流體對比蒸氣壓的差別，提出了偏心因子ω的概念
因此，任何流體的ω均可由該流體的臨界溫度Tc，pc以及Tr=0.7時的飽和蒸氣壓數據來確定。
根據ω的定義，氬、氪、氙這類簡單流體的ω=0，而其他流體ω>0（除H2、He外）。偏心因子ω表征了一般流體與簡單流體分子間相互作用的差異。
Pitzer提出的三參數對應態原理可以表述為：對於所有ω相同的流體，若處在相同的Tr和pr下，其壓縮因子Z必定相等。壓縮因子Z的關係式為
式中，Z（0）和Z（1）都是Tr和pr的函式，而偏心因子ω是第三參數。
對於非極性或弱極性的氣體，Pitzer普遍化關係式能夠提供可靠的結果，誤差小於3%；對強極性氣體則誤差達5%~10%；而對於締合氣體和量子氣體，誤差較大。
Lee和Kesler推廣lPitzer提出的關聯方法，並提出了三參數對應態原理的解析表達式：
式中，Z（0）和Z（r）分別為簡單流體和參考流體的壓縮因子，ω（r）=0.3978，該方程簡稱為L-K方程。L-K方程中，Z（0）和Z（r）都可用修正的BWR方程求得。簡單流體的方程常數由Ar、Kr和CH4的實驗數據擬合得到，參考流體的方程常數由正辛烷實驗數據得到。
可以預測，在L-K方程中，研究流體與參考流體的性質越接近，預測結果的準確性和可靠性就越高。因此採用兩個非球形參考流體有可能使研究流體與參考流體的性質儘可能接近。
