基本介紹
- 中文名:逸度係數
- 外文名:Fagucity Cofficient
- 定義:逸度與壓力的比值
- 值的大小:可以大於1,也可以小於1
- 直觀理解:可以理解為壓力的校正係數
- 套用學科:化工熱力學
逸度


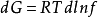

定義


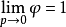
純氣體逸度係數的計算
利用狀態方程計算
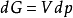



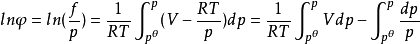
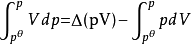
利用對應態原理計算
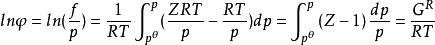






逸度表達式
RK方程
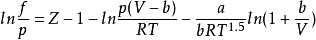
SRK方程
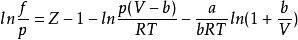
PR方程
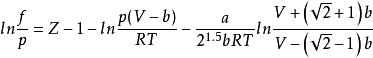
Virial方程

MH方程




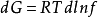



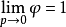
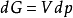



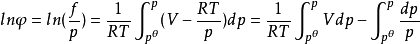
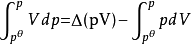
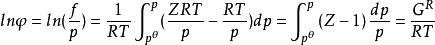






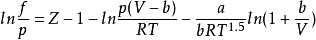
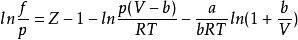
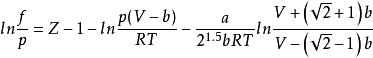


引入逸度和逸度係數的概念,對研究相平衡等非常有用,其中逸度係數是指逸度與壓力的比值。需要注意的是,理想氣體的逸度與壓力相等,另一方面,真實氣體的逸度係數是...
逸度(Fugacity)在化學熱力學中表示實際氣體的有效壓強,用 f 表示。逸度定義的出發點是化學勢與理想氣體的壓強的關係。它等於相同條件下具有相同化學勢的理想氣體的...
引入活度係數後,適用於理想溶液的各種關係可以相應修正為適用於真實溶液。類似的,逸度係數是表示真實氣體混合物中某組分和理想行為的偏離的係數。...
閃蒸參數的初值由露點參數和泡點參數內插得到。液相組元活度係數和氣相組元逸度係數的初值分別為:考慮到對於泡點, ;對於露點, , 的初值為: [3] ...
1.4.2 混合物中組分的分逸度1.5 活度和活度係數1.6 相平衡關係1.6.1 氣液相平衡1.6.2 液液相平衡參考文獻第2章 分子間作用能和位能函式...
引入活度係數後,適用於理想溶液的各種關係可以相應修正為適用於真實溶液。類似的,逸度係數是表示真實氣體混合物中某組分和理想行為的偏離的係數。 [1] ...
列出飽和水蒸氣的熱力學性質數據的表,包括在不同溫度下的飽和蒸氣壓,汽相和液相的體積、焓和熵,在不同壓力下的逸度係數。在表中還給出了不同溫度下過熱蒸汽的...
4.3 逸度和逸度係數4.3.1 逸度和逸度係數的定義4.3.2 溫度和壓力對逸度的影響4.3.3 逸度和逸度係數的計算4.3.4 液體的逸度4.4 混合過程性質變化...
3.7 逸度和逸度係數3.8 Joule-Thomoson係數3.9 均相熱力學性質計算3.10 純物質的飽和熱力學性質計算3.11 熱力學性質圖重點與難點...
3―6逸度和活度一、逸度及逸度係數二、活度及活度係數三、活度的測定思考題習題第四章 相平衡4―1相平衡條件4―2相律一、相數 獨立組分數和自由度二、相律...
2.4.2 維里係數的物理意義 2.4.3 維里係數的確定 2.4.4 由維里狀態方程導出的逸度和焓的公式 2.5 BWR狀態方程 2.6 BWRS狀態方程 2.7 基於對應狀態原理的狀...
牛頓圖是以氣體的逸變係數為縱坐標,以對比壓力π=p/pc(pc為臨界壓力)為橫坐標,繪出的等對比溫度τ=T/Tc(Tc為臨界溫度)線的圖。...
用更直觀的組分逸度係數來代替化學位,選擇相應的標準態,得到相平衡判據的第二種形式,此時要求處於平衡狀態的多相平衡體系中每個組分在各相中的逸度必須相等,這...
化工上遇到的相平衡,大都是汽(氣)液或液液相之間的平衡。關聯這些相平衡的方法,有狀態方程法和活度係數法。狀態方程法 利用狀態方程計算汽相或氣相和液相逸度的...
3.7 逸度和逸度係數 243.8 均相熱力學性質計算 253.9 純物質的飽和熱力學性質計算 263.10 熱力學性質圖表 28基本要求 28習題解析 29第4章 均相敞開系統...
3.3逸度與逸度係數的定義及其計算3.3.1逸度與逸度係數的定義3.3.2純氣體逸度的計算3.3.3逸度與溫度和壓力的關係3.3.4凝聚態物質的逸度3.4熱力學圖表...
而且流體的粘度、熱導率、分子擴散係數等物性參數,以及維里係數、逸度係數、焓、熱容等熱力學參數,也可以根據對應態原理估算,並已編繪出相應的普遍化圖表以供查...
4 6從狀態方程導出逸度係數、焓及熵計算公式4 6 1由狀態方程導出Z方程4 6 2由狀態方程導出逸度係數計算公式4 6 3由狀態方程導出熵差計算公式...
而且流體的粘度、熱導率、分子擴散係數等物性參數,以及維里係數、逸度係數、焓、熱容等熱力學參數,也可以根據對應態原理估算,編繪出相應的普遍化圖表以供查考。...
將氣相逸度係數及液相活度係數因素也一併考慮進去。這樣,就將相平衡計算變為求系統自由能最小的最佳化問題,這對於推進相平衡的計算工作是十分重要的方向;...
逸度與逸度係數逸度及逸度係數的定義氣體的逸度液體的逸度兩相系統的熱力學性質及熱力學圖表兩相系統的熱力學性質熱力學性質圖表習題...
7 2 4混合物中組分的逸度和逸度係數2107 2 5溫度和壓力對逸度的影響2167 3理想溶液和標準態2177 4流體均相混合時的性質變化219...
6 逸度係數的計算104第四節拉烏爾定律和亨利定律1051 液態混合物、溶液的液氣平衡1052 拉烏爾定律1053 亨利定律1064 拉烏爾定律與亨利定律的對比106...
5.3逸度和逸度係數965.3.1純氣體的逸度計算975.3.2純液體的逸度計算1015.3.3溶液中組分的逸度計算1035.3.4利用Microsoft Excel進行熱力學性質計算108...
3.3.2 混合工質比摩爾焓、比摩爾嫡及組元逸度係數計算3.3.3 混合工質氣液相平衡的計算3.4 工質遷移性質的計算方法3.4.1 動力黏度的計算...
附錄二 組分逸度係數方程式的推導參考資料 1. 化工熱力學 .豆瓣[引用日期2015-03-21] 詞條標籤: 文化, 出版物 圖集 化工熱力學圖冊 V百科往期回顧 詞條...
1.3.3逸度係數的計算1.3.4利用實驗數據1.4液液平衡數據1.4.1液液平衡關係1.4.2利用實驗數據1.5實驗數據的擬合第2章流體輸送和管路計算...
3.3 逸度與逸度係數3.4 兩相系統的熱力學性質及熱力學圖表4.流體混合物的熱力學性質4.1 變組成體系熱力學性質間的關係4.2 化學位和偏摩爾性質...
