雷德利希-鄺氏方程

雷德利希-鄺氏狀態方程（Redlich-Kwong equation of state），簡稱R-K方程，是物理化學中基於范德瓦耳斯方程的一個近似描述真實氣體行為的狀態方程。此方程是由猶太裔奧地利化學家奧托·雷德利希（Otto Redlich）和美國華裔學者約瑟夫·鄺（Joseph Neng Shun Kwong，1916－1998）在1949年提出的。

基本介紹

• 中文名：雷德利希-鄺氏方程
• 外文名：Redlich-Kwong equation of state

簡介

方程的一般形式為：

其中：P為氣體壓強；R為氣體常數；T為溫度； 為氣體的摩爾體積；a為常數，用於修正分子間引力；b為常數，用於修正體積。

R-K方程對烴類等非極性氣體精度較好，且適用的溫度、壓力範圍較寬。不過對極性氣體一般不適用。

R-K方程中的 不同於范德瓦耳斯方程中的常數。兩常數值可通過實驗數據回歸求得，缺乏實驗數據時也可由氣體的臨界點數據求得：

其中 分別為臨界溫度和臨界壓力。

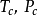
Redlich—Kwong方程

• {\displaystyle {p={\frac {R\,T}{V_{m}-b}}-{\frac {a}{{\sqrt {T}}\,V_{m}\left(V_{m}+b\right)}}}}
  
• {\displaystyle a={\frac {0.42748\,R^{2}\,T_{c}^{\,2.5}}{p_{c}}}}
  
• {\displaystyle b={\frac {0.08662\,R\,T_{c}}{p_{c}}}}
  

雷德利希-鄺氏方程於1949年被提出，是對於當時其他物態方程的一個較大的改進形式。由於它相對簡單的數學形式，它仍然引起了很多人的興趣。雖然比范德華方程更優越，但是因為它在涉及液相的情況里表現得不太好，因此不能用於精確計算氣液平衡。然而，它仍然可以在涉及單獨的液相的情況里發揮作用。

當壓強對臨界壓強的比值小於溫度對臨界溫度比值的一半時，即：

• {\displaystyle {\frac {p}{p_{c}}}<{\frac {T}{2T_{c}}}.}
  

雷德利希-鄺氏方程能夠充分勝任計算氣相屬性。

索阿維對雷德利希-鄺氏方程的修正

• {\displaystyle p={\frac {R\,T}{V_{m}-b}}-{\frac {a\,\alpha }{V_{m}\left(V_{m}+b\right)}}}
  

• {\displaystyle a={\frac {0.42748\,R^{2}\,T_{c}^{2}}{P_{c}}}}
  
• {\displaystyle b={\frac {0.08664\,R\,T_{c}}{P_{c}}}}
  
• {\displaystyle \alpha =\left(1+\left(0.48508+1.55171\,\omega -0.15613\,\omega ^{2}\right)\left(1-T_{r}^{\,0.5}\right)\right)^{2}}
  

• {\displaystyle T_{r}={\frac {T}{T_{c}}}}
  

這裡，{\displaystyle \omega }是該種物質的偏離係數。索阿維修正的原始形式為：

• {\displaystyle \alpha =\left(1+\left(0.48+1.574\,\omega -0.176\,\omega ^{2}\right)\left(1-T_{r}^{\,0.5}\right)\right)^{2}}
  

在1972年，索阿維(G. Soave）將雷德利希-鄺氏方程中的1/√(T)項替換為一個與溫度和偏離係數有關的函式α(T,ω)，替換後的方程也被稱作“索阿維-雷德利希-鄺氏方程”。引入α函式是為了與烴的蒸發壓強相適應，事實證明這個方程在這些物質的相關計算中更加精確。