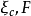立方型狀態方程

立方型狀態方程是指可展開為摩爾體積或密度的三次方程式，這類方程式形式簡單，能夠用解析法求解，精確度較高，給工程套用帶來方便。最早的Van der Waals狀態方程是於1873年提出的，後來又有了Redlich Kwong 方程、Soave Redlich Kwong方程、Peng Robinson 方程、Patel Teja 方程，使得精度不斷提高。對於方程的求解，雖然立方型狀態方程是可以用解析法來求解三個體積根的，但工程計算通常採用疊代法來求解。

基本介紹

• 中文名：立方型狀態方程
• 外文名：cubic equations of state
• 定義：可展開為摩爾體積的三次方程式
• 最早形式：Van der Waals狀態方程
• 其它類型：RW方程、SRW方程、PR方程等
• 套用領域：化工熱力學

方程類型

Van der Waals 狀態方程

1873年J.D. Van der Waals提出了第一個適用於真實氣體的狀態方程，可寫為：

其中a,b是各種物質特有的常數，與其臨界參數有關。

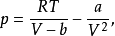
Van der Waals方程是最簡單的立方型狀態方程。該方程能定量地描述流體的P-V-T關係，能夠同時描述氣、液兩相的性質。雖然精確度不高，但還是特別值得關注，因為它建立方程的推理方法對立方型方程、對比態原理以及後來與之類似的狀態方程的開發有著巨大的貢獻。

Redlich Kwong 方程

該方程由Redlich和Kwong於1949年提出，簡稱為RK方程，其形式如下：

其中a,b為RK常數，與流體的特性有關。

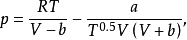
RK方程與Van der Waals方程的區別僅在於壓力修正項的形式不同。

Soave Redlich Kwong方程

SRK方程，其形式為：

其中 是臨界參數有關的常數； 是對比溫度 的函式，其中的參數F可由純物質的飽和蒸氣壓和液體的密度數據關聯得到，對於非極性或弱極性物質，F可以通過下式進行計算：

其中ω為偏心因子。

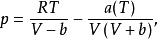
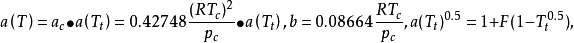
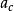
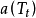
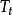
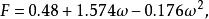
與RK方程相比，SRK方程顯示出很大的優越性，特別是用它來計算純烴和烴類混合物系統的氣液平衡具有較高的精度，該方程在烴套用方面做出了很大的貢獻。

Peng Robinson 方程

RK和SRK方程有一個共同的不足，就是預測液相摩爾體積時精度相當差。為了彌補這一不足，Peng和Robinson 於1976年提出了如下形式的狀態方程：

。

PR方程中的 是對比溫度 的函式，其中的參數F可由純物質的飽和蒸氣壓與飽和液體的密度數據關聯得到，對於非極性或弱極性物質，F亦可以通過下式計算：

。

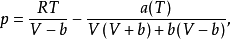
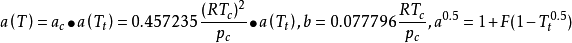
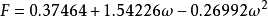
PR方程的臨界壓縮因子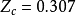 ，該值比RK方程的0.333有明顯改進，但仍偏離真實流體的數值。PR方程計算飽和蒸氣壓、飽和液體密度和氣液平衡的準確度均高於SRK方程。值得指出的是，SRK方程和PR方程在預測流體的蒸氣壓時顯示出突出的優勢，其主要原因在於溫度函式a(T)的表達式。

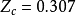
Patel Teja 方程

1982年，由Patel 和Teja導出了Patel Teja方程，其形式為：

其中 的計算方法如下：

是下列方程的最小正根：。

這兩個參數是由純物質的飽和蒸氣壓和飽和密度數據關聯得到的，對非極性或弱極性物質也可由以下兩個式子求得：

。

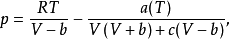
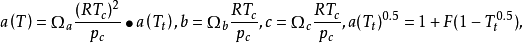
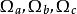
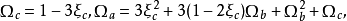
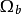
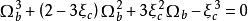
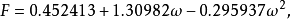
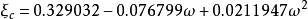
通用形式

一般式

立方型狀態方程可歸納為如下形式：

其中，對於不同的立方型狀態方程，m,n取不同的值，並且滿足如下關係：

其中 為關聯常數， 均為與臨界性質有關的參數。

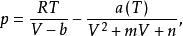
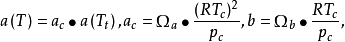
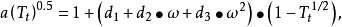
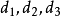
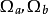
各方程對應參數值

（1）Van der Waals方程：m=0，n=0， ；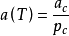

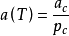
（2）Redlich Kwong 方程：m=b，n=0， ；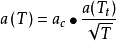

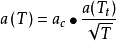
（3）Soave Redlich Kwong方程：m=b，n=0， ；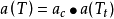

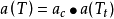
（4）Peng Robinson 方程：m=2b， ， ；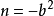

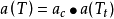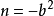
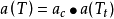
（5）Patel Teja 方程：m=b+c，n=-bc， 。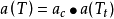

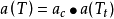
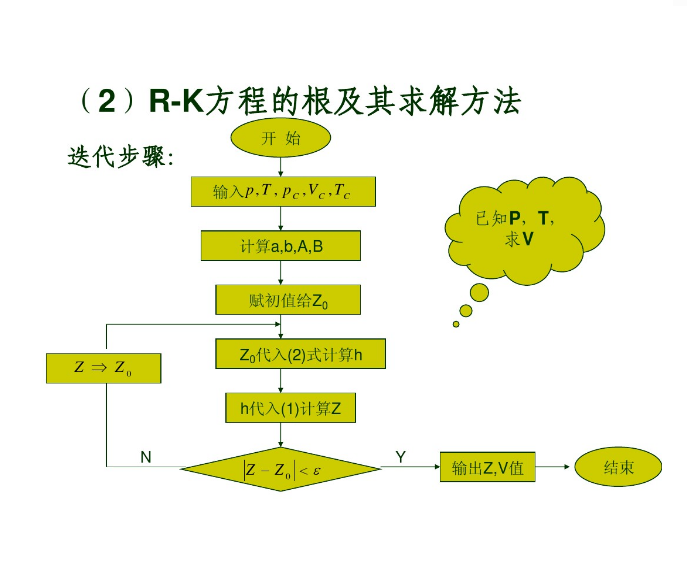
方程的求解

雖然立方型狀態方程可以用解析法求解三個體積根，但工程計算通常採用疊代法。下面具體介紹疊代過程，以Peng Robinson 方程為例進行討論。

已知：

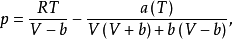
為便於疊代，將上式恆等變形，得到：

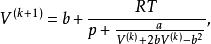
利用上式進行疊代計算時，體積根的初值設定方法為：

（1）對於氣相，取初值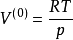 ，即以理想氣體作為初值；

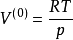
（2）對於液相，取初值 。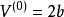

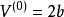
計算出初值後代入上式右端，在疊代收斂後即可得到氣相摩爾體積或液相摩爾體積。

套用

立方型狀態方程的套用：

（1）用一個EOS即可精確地代表相當廣泛範圍內的實驗數據，藉此可精確計算所需的數據；

（2）EOS具有多功能性，除了pVT性質之外，還可用最少量的數據計算流體的其他熱力學函式、純物質的飽和蒸氣壓、混合物的氣一液相平衡、液一液相平衡．尤其是高壓下的相平衡計算；

（3）在相平衡計算中用一個EOS可進行兩相、三相的平衡數據計算，狀態方程中的混合規則與相互作用參數對各相使用同一形式或同一數值，計算過程簡捷、方便。