伴隨勒讓德多項式

伴隨勒讓德多項式（Associated Legendre polynomials，又譯締合勒讓德多項式、連帶勒讓德多項式、關聯勒讓德多項式）是數學上對常微分方程解函式序列的稱呼，在數學和理論物理學中有重要的意義。

基本介紹

• 中文名：伴隨勒讓德多項式
• 外文名：Associated Legendre polynomials
• 分類：數學物理、微分方程
• 領域：數理科學

定義

數學上對如下形式常微分方程解函式序列：

該方程是在球坐標系下求解拉普拉斯方程時得到的，因上述方程僅當 和 均為整數且滿足 時，才在區間 [−1, 1] 上有非奇異解，所以通常把 和 均為整數時方程的解稱為伴隨勒讓德多項式；把 和 為一般實數或複數時方程的解稱為廣義勒讓德函式（generalized Legendre functions）。

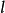
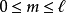
當 為整數時，方程的解即為一般的勒讓德多項式。

注意當 m 為奇數時，連帶勒讓德多項式並不是多項式。

正交性

與勒讓德多項式一樣，伴隨勒讓德多項式在區間 [-1,1] 上也滿足正交性。

這是因為，與勒讓德方程一樣，伴隨勒讓德方程也是施圖姆-劉維爾型的：

正交性的另一種表述如下，它與下面提到的球諧函式有關。

與勒讓德多項式的關係

伴隨勒讓德多項式可以由勒讓德多項式求m次導得到：

等號右邊的上標 (m) 表示求m次導。

與超幾何函式的關係

伴隨勒讓德函式（即 l, m 不一定要是整數）可以用高斯超幾何函式表達為：

注意 μ 為正整數 m 時 1-μ 是伽瑪函式的奇點，此時等號右邊的式子應該理解為當 μ 趨於 m 時的極限。

負數階連帶勒讓德多項式

顯然伴隨勒讓德方程在變換m→-m下保持不變，傳統上習慣定義負數階伴隨勒讓德多項式為：

容易驗證，這樣定義的伴隨勒讓德多項式能夠使得上面的正交關係可以推廣到 m 為負數的情況。

注意在個別文獻（如圖1）中會直接取

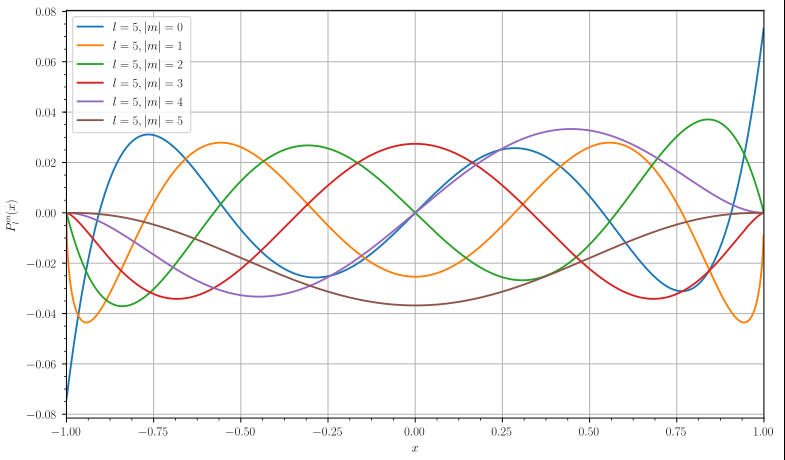圖1 l=5時連帶勒讓德多項式的圖像

與球諧函式的關係

球諧函式是球坐標下三維空間拉普拉斯方程的角度部分的解，構成一組完備的基組，有著重要的意義。採用本文中定義的伴隨勒讓德多項式的表達式，球諧函式可以表達為：

由伴隨勒讓德多項式的正交關係可以直接得到球諧函式的正交關係：

式中 dΩ 是立體角元。