基本介紹
- 中文名:球對稱位勢
- 外文名:Particle in a spherically symmetric potential
- 領域:量子力學
簡介
薛丁格方程





角部分解答


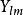
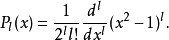
徑向部分解答








參閱
- Delta位勢阱







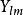
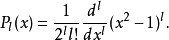








球對稱位勢乃是一種只與徑向距離有關的位勢。許多描述宇宙相互作用的基本位勢,像重力勢、電勢,都是球對稱位勢。這條目只講述,在量子力學裡,運動於球對稱位勢...
在量子力學裡,Delta位勢壘是一個壘內位勢為狄拉克Delta函式,壘外位勢為0的位...有限位勢壘 球對稱位勢 Delta位勢阱 量子隧穿效應 參考資料 1. T.C....
通常,在經典力學裡,一維的有限位勢壘問題會設定一個粒子,從位勢壘的左邊,往位...有限位勢壘參閱術語 編輯 自由粒子 無限深方形阱 有限深方形阱 球對稱位勢...
其中()是球對稱的位勢,和分別為核的自旋角動量和軌道角動量,()是自旋軌道耦合勢的形狀因子。按照量子力學,對於這個平均場,存在一系列不連續的能級。 圖中示意地...
用來描述與分析擁有球狀對稱性質的物理問題,最自然的坐標系,莫非是球坐標系。例如,一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式,拉普拉斯方程與...
用來描述與分析擁有球狀對稱性質的物理問題,最自然的坐標系,莫非是球坐標系。例如,一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式,拉普拉斯方程與...
用來描述與分析擁有球狀對稱性質的物理問題,最自然的坐標系,莫非是球坐標系。例如,一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式,拉普拉斯方程與...
其為量子力學中數個重要的模型系統中的一者,因為一任意勢在穩定平衡點附近可以...有限位勢壘 球對稱位勢 Delta位勢壘 參考資料 1. Griffiths, David J. ...
類氫原子 球對稱位勢 拉普拉斯-龍格-楞次矢量 解讀詞條背後的知識 蝌蚪五線譜 北京市科協主辦科普網站 π是如何計算的?去問氫原子啊! 圖片來源:Benjamin ...
在原子物理學涉及旋轉對稱性(rotational symmetry)的理論里,角動量算符占有中心的...球對稱位勢拉普拉斯-龍格-楞次矢量參考資料 1. Introductory Quantum Mechanics,...
在物理學裡,無限深方形阱(infinite square potential),又稱為無限深位勢阱(...球對稱位勢 Delta 位勢阱 Delta 位勢壘 量子隧穿效應 盒中氣體 ...
在量子力學裡,有限深方形阱,又稱為有限深位勢阱,是無限深方形阱的延伸。有限...有限位勢壘 球對稱位勢 Delta位勢阱 Delta位勢壘 量子隧穿效應 ...
