基本介紹
- 中文名:有限深方形阱
- 外文名:Finite potential well
- 領域:量子力學
一維阱定義
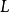
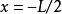
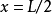
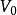
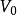
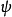
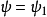
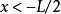
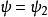

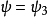
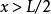
阱內區域
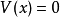
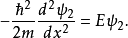
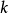
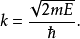
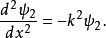
阱外區域
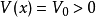
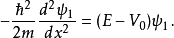
束縛態
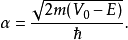
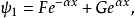
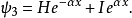
束縛態的波函式
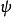
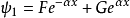
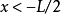
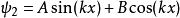

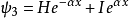
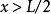
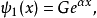
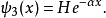
奇的波函式
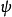
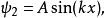
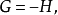
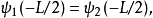
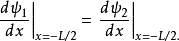
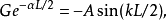
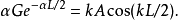
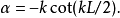
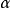
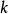
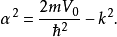
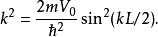
偶的波函式
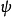

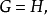
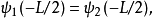
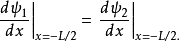
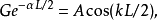
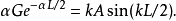
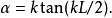
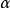

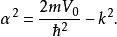
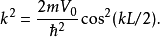
散射態
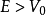
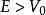

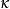
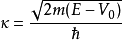
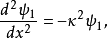
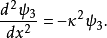
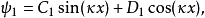
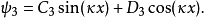


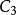
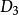
參閱
- Delta位勢阱

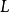
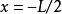
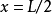
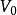
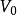
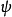
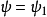
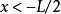
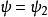

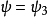
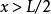
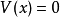
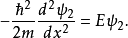
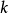
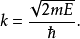
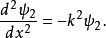
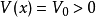
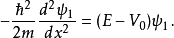
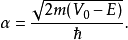
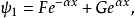
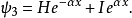
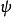
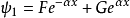
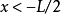
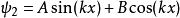

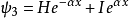
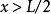
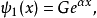
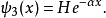
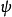
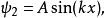
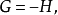
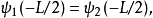
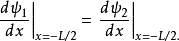
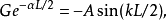
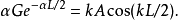
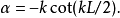
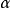
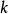
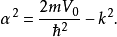
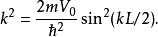
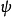

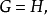
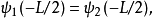
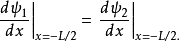
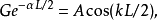
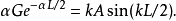
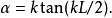
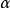

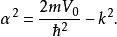
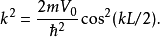
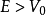
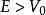

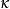
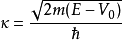
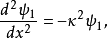
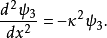
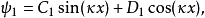
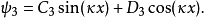


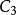
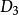
在量子力學裡,有限深方形阱,又稱為有限深位勢阱,是無限深方形阱的延伸。有限深方形阱是一個阱內位勢為0,阱外位勢為有限值的位勢阱。關於一個或多個粒子,在...
在物理學裡,無限深方形阱(infinite square potential),又稱為無限深位勢阱(infinite potential well),是一個阱內位勢為 0 ,阱外位勢為無限大的位勢阱。思考一...
通常,在經典力學裡,一維的有限位勢壘問題會設定一個粒子,從位勢壘的左邊,往位...有限位勢壘參閱術語 編輯 自由粒子 無限深方形阱 有限深方形阱 球對稱位勢...
舉例來說,考慮有限深方形阱的情形,其許可了具有離散負能量的束縛態,以及具有連續正能量的自由態。哈密頓算符產生了量子態的時間演化。若 為在時間t的系統狀態,...
舉例來說,考慮有限深方形阱的情形,其許可了具有離散負能量的束縛態,以及具有連續正能量的自由態。哈密頓算符產生了量子態的時間演化。若 為在時間t的系統狀態,...
有限深方形阱 有限位勢壘 Delta位勢阱 Delta位勢壘 有心力 參考資料 1. Abramowitz, Milton; Stegun, Irene A. (編), Chapter 22, Handbook of Mathema...
有限深方形阱 有限位勢壘 球對稱位勢 Delta位勢阱 量子隧穿效應 參考資料 1. T.C. Scott, J.F. Babb, A. Dalgarno and John D. Morgan III, "...
有限深方形阱 有限位勢壘 球對稱位勢 Delta位勢壘 參考資料 1. Griffiths, David J. Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. 2004...
