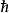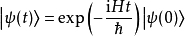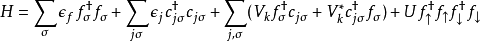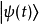安德森模型是一種哈密頓算符，通常用來描述重費米子。
基本介紹
- 中文名：安德森模型
- 外文名：Anderson model
- 提出時間：1978年
- 用來：描述重費米子
- 提出者：菲利普·安德森
簡介,圖示,哈密頓算符,相關條目,
簡介
安德森模型是對瑟利模型的擴展和修正：即，該模型在瑟利模型之上增加了一組問題，涉及的是危險線索的來源及可察覺性、運行系統內的撥動（機械運行過程及環境狀況的不穩定性），以及控制和減少這些撥動使之與人的行為過程相一致。因此，安德森模型與瑟利模型可成為一個更為完整的模型。
圖示
下圖所示：
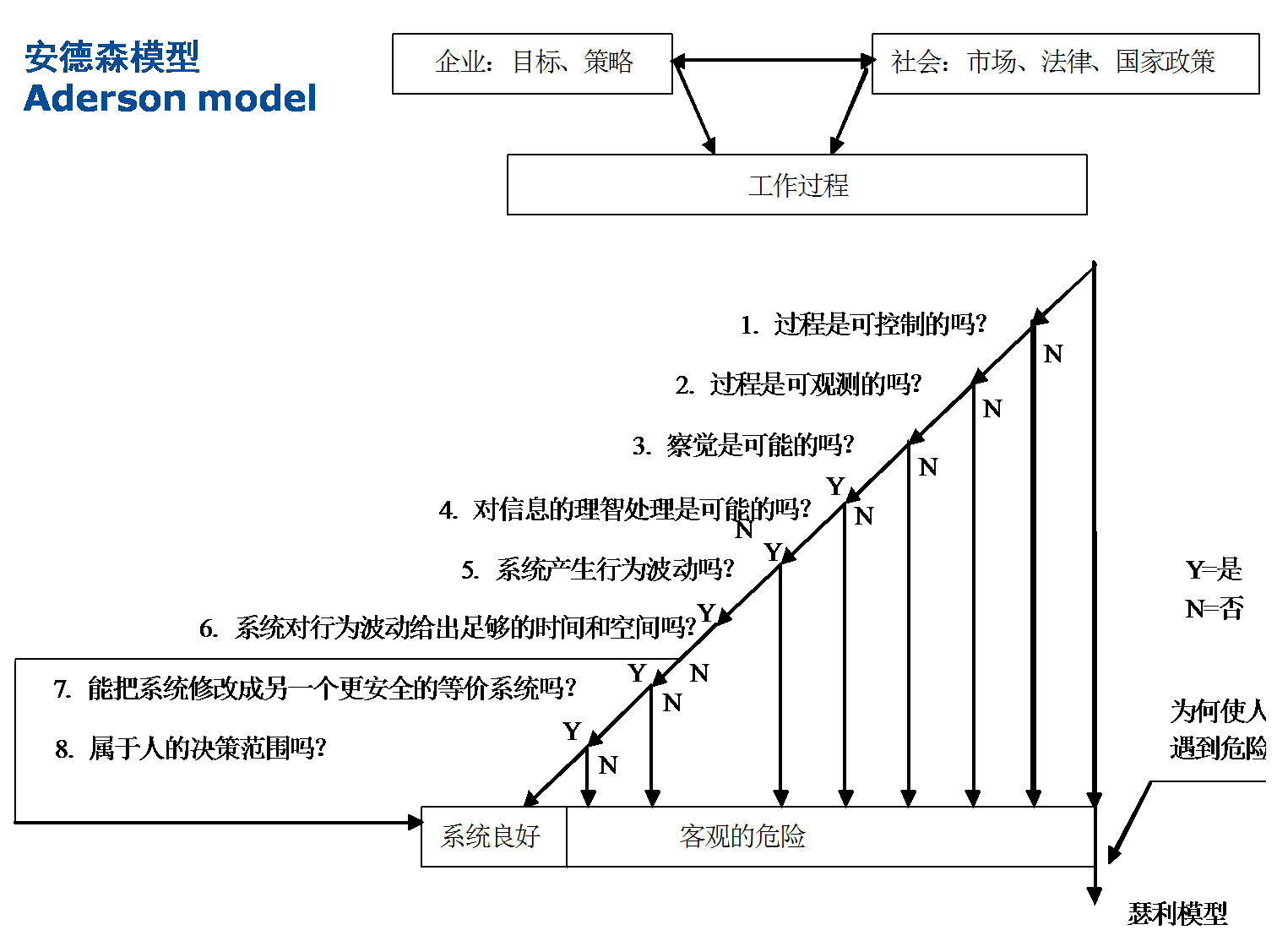安德森模型哈密頓算符
量子力學中，哈密頓算符（英語：Hamiltonian，縮寫符號：H或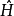
） 為一個可觀測量，對應於系統的總能量。一如其他所有算符，哈密頓算符的譜為測量系統總能是所有可能結果的集合。如同其他自伴算符，哈密頓算符的譜可以透過譜測度（spectral measure）被分解，成為純點（pure point）、絕對連續（absolutely continuous）、奇點（singular）三種部分。純點譜與本徵矢量相應，而後者又對應到系統的束縛態（bound states）。絕對連續譜則對應到自由態（free states）。奇點譜則很有趣地由物理學上不可能的結果所組成。舉例來說，考慮有限深方形阱的情形，其許可了具有離散負能量的束縛態，以及具有連續正能量的自由態。
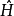
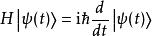
其中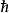
為約化普朗克常數。此方程為薛丁格方程。（其與哈密頓-雅可比方程具有相同形式，也因為此，H冠有哈密頓之名。）若給定系統在某一初始時間（t= 0）的狀態，我們可以積分得到接下來任何時間的系統狀態。其中特別的是，若H與時間無關，則
