基本介紹
- 中文名:量子諧振子
- 外文名:quantum harmonic oscillator
- 領域:量子力學
一維諧振子
哈密頓算符與能量本徵態




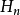


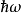

階梯算符方法
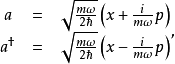
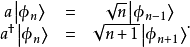



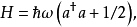
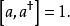
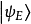

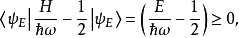
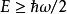

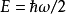

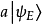
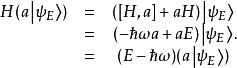
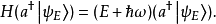
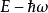



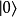
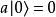
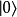
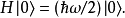

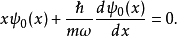
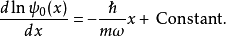

自然長度與能量尺度
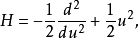

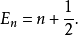
案例:雙原子分子
N維諧振子


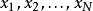

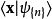
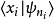






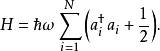
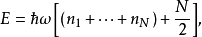

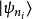
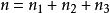

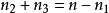


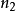

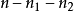
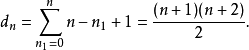

耦合諧振子








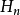


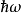

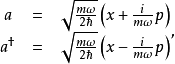
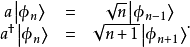



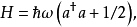
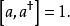
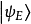

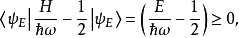
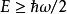

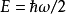

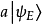
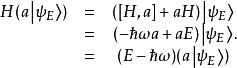
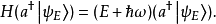
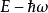



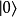
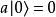
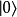
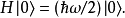

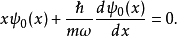
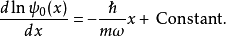

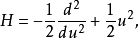

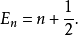



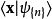
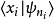






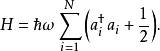
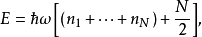

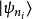
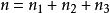

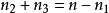


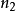

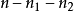
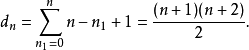





在量子力學裡,量子諧振子(英語:quantum harmonic oscillator)是經典諧振子的延伸。其為量子力學中數個重要的模型系統中的一者,因為一任意勢在穩定平衡點附近可以用...
普朗克進一步假設單獨量子諧振子吸收和放射的輻射能是量子化的,這一觀點嚴重地衝擊了經典物理學。量子論涉及物質運動形式和運動規律的根本變革。首先注意到量子假設有...
線性諧振子是物理學中一個重要的模型,許多在平衡點附近振動的物理問題都可簡化為線性諧振運動。一般說來,任何一個體系在穩定平衡點附近都可以近似地用線性諧振子來...
第1章量子力學基礎 第2章波函式與薛丁格方程 第3章一維勢場模型 第4章一維勢場模型的套用 第5章量子諧振子 第6章諧振子模型的套用 第7章力學量的算...
第2章 IEO方法研究諧振子系統能級2.1 一維有坐標-動量耦合的量子諧振子2.2 二維耦合量子諧振子2.3 奇異諧振子模型2.4 奇異參量放大器諧振子模型...
這與量子諧振子的哈密頓算符基本一致,但勢能的最小值需要在位置表象中移動x0=ħky/mωc。為了得出能量,我們假設對於諧振子勢能的平移並不會影響到系統的能量,...
特別小的振諧子,如振動著的分子,不受摩擦,能量不會逐步消耗,但只能呈現為分立值,這種量子化的諧振子,最早是由德國物理學家M.普朗克提出的,用以成功地解釋了...
第5章量子諧振子 第6章諧振子模型的套用 第7章力學量的算符表示 第8章三維空間的量子力學 量子力學Ⅱ詞條標籤: 文化, 出版物 圖集...
愛因斯坦模型是一種固體模型,基於三種假設:1.晶格中的每一個原子都是三維量子諧振子;2.原子不互相作用;3.所有的原子都以相同的頻率振動(與德拜模型不同)。第一...
在普通量子力學中,零點能量是系統基態所具有的能量。這樣的例子中最有名的是量子諧振子基態所具有的能量 零點能量公式 。更精準地說,零點能量是此系統哈密頓算符...
但是在詮釋這個公式時,通過將物體中的原子看作微小的量子諧振子,他不得不假設這些量子諧振子的總能量不是連續的,即總能量只能是離散的數值(經典物理學的觀點恰好...
在組合數學中,埃爾米特多項式是阿佩爾方程的解。物理學中,埃爾米特多項式給出了量子諧振子的本徵態。 [1] 中文名 埃爾米特多項式 外文名 Hermite polynomial ...
例如常採用經典力學或者半經典近似處理原子核運動;在振動幅度較小的情況下,可將勢能面近似為二次曲面,而原子核的運動則轉化為量子諧振子問題而可解析解出。某些...
量子場論的二次量子化程式要求球與彈簧的組合是呈現量子化的,也就是說場強度在空間中每一點被量子化。正則式地(Canonically)來說,空間中每點的場是個諧振子,...
