基本介紹
- 中文名:冪級數
- 外文名:Power series
- 作用:數學分析
- 對象:級數
- 領域:實變函式、複變函數等
- 定義1:函式列 , 則稱為函式項級數。
概念



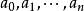

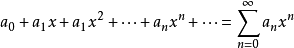

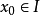
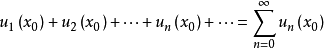


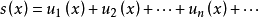

收斂半徑
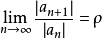

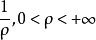
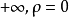
運算
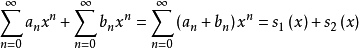
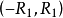
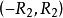
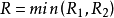
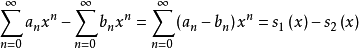
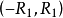
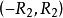
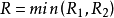

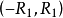
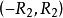
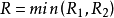
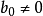
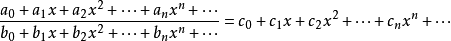
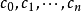
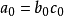
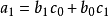

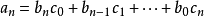

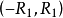
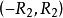





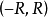
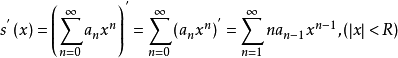

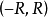




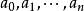

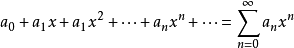

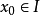
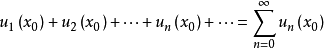


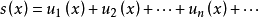

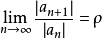

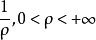
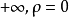
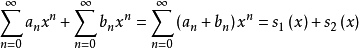
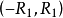
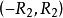
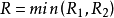
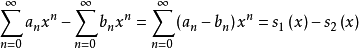
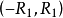
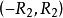
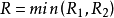

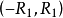
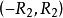
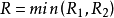
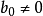
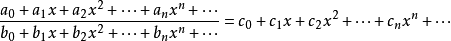
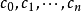
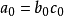
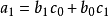

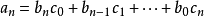

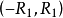
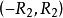





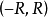
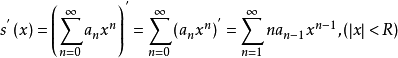

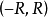
冪級數,是數學分析當中重要概念之一,是指在級數的每一項均為與級數項序號n相對應的以常數倍的(x-a)的n次方(n是從0開始計數的整數,a為常數)。冪級數是數學...
弗雷歇冪級數簡稱F冪級數,是通常冪級數一種較強意義下的無窮維推廣形式。...... 弗雷歇冪級數簡稱F冪級數,是通常冪級數一種較強意義下的無窮維推廣形式。...
加托冪級數簡稱G冪級數,是通常冪級數一種較弱意義下的無窮維推廣形式。...... 加托冪級數簡稱G冪級數,是通常冪級數一種較弱意義下的無窮維推廣形式。...
冪級數解法是求解常微分方程的一種方法,特別是當微分方程的解不能用初等函式或或其積分式表達時,就要尋求其他求解方法,尤其是近似求解方法,冪級數解法就是常用的...
廣義冪級數是冪級數的推廣。廣義冪級數的表達式中cn(n=0,±1,...)均為復常數,還可給出不同形式的廣義冪級數。...
無窮級數是研究有次序的可數或者無窮個數函式的和的收斂性及和的數值的方法,理論以數項級數為基礎,數項級數有發散性和收斂性的區別。只有無窮級數收斂時有一個和...
冪級數概念在多元微積分學中的一個推廣是多元冪級數...... 冪級數概念在多元微積分學中的一個推廣是多元冪級數 冪級數概念在多元微積分學中的一個推廣是多元冪...
麥克勞林級數(Maclaurin series)是函式在x=0處的泰勒級數,它是牛頓(I.Newton)的學生麥克勞林(C.Maclaurin)於1742年給出的,用來證明局部極值的充分條件,他自己說明...
級數是指將數列的項依次用加號連線起來的函式。典型的級數有正項級數、交錯級數、冪級數、傅立葉級數等。級數理論是分析學的一個分支;它與另一個分支微積分學一...
對數級數(logarithmic series),即對數函式的冪級數展開式。...... 對數級數(logarithmic series),即對數函式的冪級數展開式。這個級數由梅卡托(Mercator, N.)發表於...
在數學中,泰勒級數(英語:Taylor series)用無限項連加式——級數來表示一個函式,這些相加的項由函式在某一點的導數求得。泰勒級數是以於1715年發表了泰勒公式的...
三體問題冪級數解(power series solution ofthree-body problem)三體問題的一種解.指宋德曼(Sundman,K. F.)於1913年提出的一般三體問題的解,此解可以展開為...
在數學內,墨卡托級數(Mercator series)或者牛頓-墨卡托級數(Newton–Mercator series)是一個自然對數的泰勒級數。...
朗伯級數是一種特殊形式的級數,也譯作蘭伯特級數等,形如∑∞n-1(anxn/(1-xⁿ))的函式項級數,其中an,x為實數,若∑an收斂,則當x≠±1時,該級數收斂;若...
在數學中,複變函數f(z)的洛朗級數,是冪級數的一種,它不僅包含了正數次數的項,也包含了負數次數的項。有時無法把函式表示為泰勒級數,但可以表示為洛朗級數。...
調和級數(英語:Harmonic series)是一個發散的無窮級數。調和級數是由調和數列各元素相加所得的和。中世紀後期的數學家Oresme證明了所有調和級數都是發散於無窮的。...
歐拉級數是各項為質數倒數的級數,歐拉(Euler,L.)於1748年證明了歐拉級數是發散的,同時給了質數集是無窮集的一個證明。...
優級數法最初被柯西Cauchy,A.-L.)用來研究複變函數的解析性,後經布里奧(Briot,C.A.A.)和布凱(Bouquet,J.-C.)之手,被發展成一種研究微分方程的有效方法...
一方面能藉助級數表示許多常用的非初等函式, 微分方程的解就常用級數表示;另一方面又可將函式表為級數,從而藉助級數去研究函式,例如用冪級數研究非初等函式,以及進行...
Volterra 級數是一種泛函級數,由義大利數學家Volterra於1880年首先提出,當時是作為對Taylor級數的推廣而提出的。...
泰勒定理開創了有限差分理論,使任何單變數函式都可展成 冪級數;同時亦使 泰勒成了有限差分理論的奠基者。泰勒於書中還討論了 微積分對一系列物理問題之套用,其中...
