基本介紹
- 中文名:冪級數解法
- 外文名:power series method
- 所屬學科:數學
- 套用:求解常微分方程的一種方法
一階微分方程的冪級數求解
基本方法
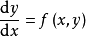

例題解析
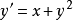
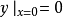
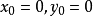

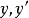
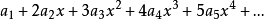

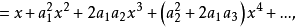
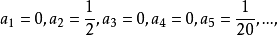
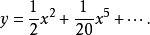
二階齊次線性方程的冪級數解法
定理

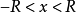
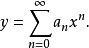
求解方法
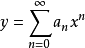
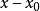
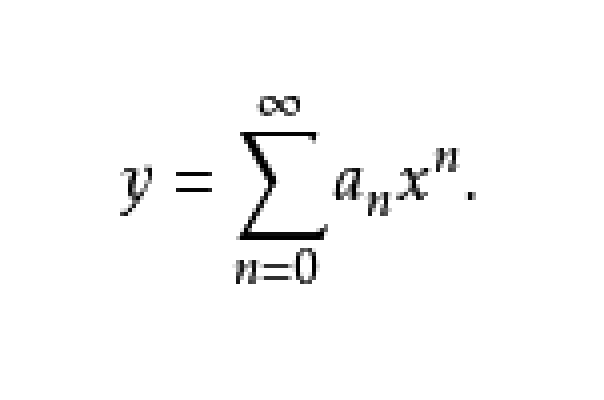
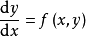

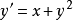
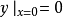
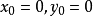

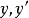
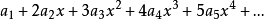

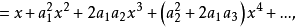
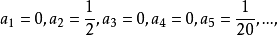
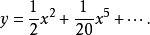

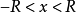
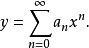
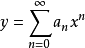
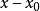
冪級數解法是求解常微分方程的一種方法,特別是當微分方程的解不能用初等函式或或其積分式表達時,就要尋求其他求解方法,尤其是近似求解方法,冪級數解法就是常用的...
全書仍為十一章,各章內容為:基本概念;初等積分法;存在和唯一性定理;奇解;高階微分方程;線性微分方程組;冪級數解法;定性理論與分支理論初步;邊值問題;首次積分;...
求解超越方程的近似解法有很多,圖象法雖然形象,但得到的解誤差太大了。常用的近似解法有牛頓切線法、冪級數解法等等,也可以編制一段程式用計算機求解,或者利用現成...
複變函數論主要討論解析函式的微分、積分、冪級數展開、留數理論以及共形映射等內容.二階線性常微分方程的冪級數解法雖然是在解析函式的冪級數展開的基礎上得到的,...
換言之,形式解陣中的一切形式對數和均收斂。這個結果能使人們寫出方程的解結構的一般形式,因而也就構成線性方程冪級數解法的理論基礎。...
二、條件極值拉格朗日乘數法 二、微分方程的冪級數解法 習題9-8 三、歐拉公式 *第九節二元函式的泰勒公式 習題12-5 一、二元函式的泰勒公式 *第六節函式項級數...
第八節 冪級數解法大意 主要內容 疑難解析 方法、技巧與典型例題分析 第四章 線性微分方程組 第一節 一階微分方程組線性微分方程組的一般概念 主要內容...
4.4 變係數線性向分方程4.5 冪級數解法4.6 套用實例第五章 常微分方程線5.1 一階微分方程線5.2 線性微分方程的一般概念及理論5.3 常係數齊次線性微分方程組...
11.1 二階常微分方程的冪級數解法233 11.1.1 冪級數解法理論概述233[1] 參考資料 1. 數學物理方法與仿真 .豆瓣讀書[引用日期2013-01-27] 詞條...
微分方程的冪級數解法 習題-11 *第十二節 常係數線性微分組解法 *習題12-12 總習題 習題答案與提示 [1] 高等(第五版)教學資源 編輯 教材 ...
5常係數二階線性微分方程 6線性系統 7冪級數解法 8數值計算方法[1] 參考資料 1. 高等數學講義 .豆瓣讀書[引用日期2013-09-09] 詞條標籤: 出版物 , 書籍 圖...
7.2.5 數值解法7.2.6 方向場7.2.7 正交軌線7.3 Maple套用於解高階方程和方程組7.3.1 用Maple解高階線性方程7.3.2 高階線性方程的冪級數解法...
4.2.2常係數線性齊次微分方程的解法4.2.3某些變係數線性齊次微分方程的解法習題4.24.3二階線性齊次微分方程的冪級數解法4.3.1引言4.3.2常點鄰域內的冪級數解...
12.11 微分方程的冪級數解法習題解答與提示參考文 [2] 參考資料 1. 高等數學.下冊 .豆瓣讀書[引用日期2013-10-21] 2. . ..[引用日期2016-03-06]詞條...
7.2冪級數 7.3傅立葉級數 第八章 常微分方程 8.1一階微分方程的解法 8.2可降階的高階微分方程 8.3線性微分方程 8.4微分方程的冪級數解法與微分方程的套用...
§4.3 n階常係數線性非齊次方程解法 §4.4 可以化為常係數的變係數線性方程 §4.5 二階常係數線性方程與振動現象 §4.6 冪級數解法大意 綜合練習題4 本...
當一個函式方程或微分方程的解能展開成冪級數時,我們就說這個方程可以用冪級數解法來求解。如果這個函式方程或微分方程的冪級數解有正的收斂半徑,就稱這個冪級數解...
*11.12微分方程的冪級數解法習題11.12*11.13線性微分方程組習題11.13總習題11第12章差分方程12.1差分及差分方程的概念12.1.1差分的定義...
11.微分方程的冪級數解法12.綜合提高題型 [1] 參考資料 1. 吉米多維奇高等數學習題精選精解 .山東科學技術出版社[引用日期2016-10-26] ...
《常微分方程》是為綜合性大學與師範類院校的數學類專業編寫的常微分方程教材,內容包括基本概念、初等積分法、存在、唯一性定理、二階微分方程、冪級數解法、拉普拉斯...
3.常微分方程的冪級數解法(1474―1481) 4.微分方程組(1482―1511) 5.常微分方程的數值解(1512一1515) 6.拉普拉斯變換法(1516―1520) 附錄 微積分簡史 漢英對...
4.3.2 二階線性微分方程的冪級數解法4.3.3 第二宇宙速度計算本章學習要點常微分方程第五章 線性微分方程組 §5.1 存在唯一性定理...
6. 冪級數解法,圓孔7. Cauchy型積分解法,橢圓孔8. Riemann-Hilbert連線問題的套用,直線裂紋9. Melan 問題10. 橢圓夾雜第十章 Michell 問題...
,引導讀者形成高層次的數學直覺,從而可以直觀地學習數學物理方程的各種主要解法。...0.5 冪級數:函式的一種統一的解析表示形式 0.6 解析幾何中的數形結合思想—...
二階常係數線性微分方程三、可化為常係數線性方程的方程――歐拉方程四、冪級數解法與常數變易法16.5微分方程套用舉例一、物理問題套用二、幾何問題套用三、微小量...
二階線性常微分方程的冪級數解法和斯圖姆 劉維爾本徵值問題; 貝塞爾函式和勒讓德函式的定義、性質與套用; 求解定解問題的行波法、積分變換法和格林函式法等。 ...
2.二階常係數線性微分方程的解法 習題112 4微分方程的冪級數解法 習題11.3 5微分方程的套用 習題11.4 習題答案與提示詞條...
一階微分方程的解法可降階的微分方程的解法線性微分方程解的結構二階常係數線性微分方程的解法微分方程的冪級數解法差分與差分方程的概念...
6.1.1冪級數解法6.1.2貝塞爾函式習題6.16.2貝塞爾函式的性質6.2.1貝塞爾函式的遞推公式6.2.2貝塞爾函式的零點與正交模6.2.3函式按貝塞爾函式系展開習題6...
一、泰勒級數的概念二、函式展開成冪級數的方法 習題9-5第六節 函式的冪級數展開式的套用一、近似計算二、歐拉公式三、微分方程的冪級數解法 習題9-6...
