優級數法最初被柯西Cauchy,A.-L.)用來研究複變函數的解析性，後經布里奧(Briot,C.A.A.)和布凱(Bouquet,J.-C.)之手，被發展成一種研究微分方程的有效方法。
基本介紹
- 中文名：優級數法
- 外文名：majoriant series method
- 適用範圍：數理科學
簡介,步驟,實例,總結,
簡介
優級數法是研究解的解析性的重要方法之一。
優級數法最初被柯西Cauchy,A.-L.)用來研究複變函數的解析性，後經布里奧(Briot,C.A.A.)和布凱(Bouquet,J.-C.)之手，被發展成一種研究微分方程的有效方法。優級數則是其中的一個重要工具。
優級數法後來被西格爾(Siegel,C.L.)用於三體問題的研究，以至後來又被阿諾爾德和莫澤(Moser,J.K.)成功地發展成一種非線性問題的廣泛而有效的方法—KAM(Kolmogolov-Arnold-Moser)方法。
步驟
實例
用一個布里奧與布凱的例子說明此法。
設要求解一階偏微分方程
其中A(x,y)為(0,0)∈C×C鄰域內的已知全純函式，H(x,y)為(0,0)∈C×C鄰域內待求全純函式，記
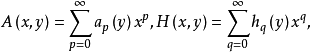其中ap為y的收斂冪級數，h0為給定冪級數，hq(q≥1)為未知冪級數。
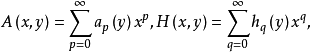
將A與H代入一階偏微分方程，再令兩邊同冪項相等，得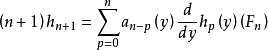
其中n為非負整數，此式顯示可由h0,a0,a1,…歸納地確定h1,h2,h3,...，故H的惟一性是明顯的。
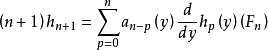
餘下要證明H的收斂性。若級數u的每一係數的模大於另一級數v的相應係數的模，
則稱級數u優於級數v，記為u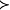
v（顯然，u的係數均為非負），考慮下式
若其中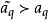
（對一切q），即
，又
，則顯然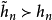
（對一切n≥1），從而有
。
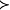
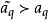
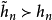
由上述討論可知，當A在(0,0)∈C×C之某一鄰域中為解析時，則它有一優級數
其中M，c為正實數。今考慮
，令其中
又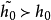
，則其解將定義一收斂級數
於是H顯然為解析，又優於H，故H必為收斂。
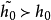
總結
綜上所述，優級數法主要由兩個步驟組成：假設方程有一個形式級數解，需證明它的係數被惟一確定；其次造一個優級數，用以證明形式級數收斂。
