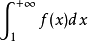概述 無窮級數是研究有次序的可數無窮個函式的和的
收斂 性及其
極限 值的方法,理論以
數項級數 為基礎,數項級數有發散性和收斂性的區別。無窮級數收斂時有一個唯一的和;發散的無窮級數沒有極限值,但有其他的求和方法,如歐拉和、切薩羅和、博雷爾和等等。
算術的加法可以對有限個數求和,但無法對無限個數求和,有些數列可以用無窮級數方法求和。可用無窮級數方法求和的包括:數項級數、函式項級數(又包括
冪級數 、
傅氏級數 ;
複變函數 中的
泰勒級數 、
洛朗級數 。
歷史 英國
曼徹斯特大學 和
埃克塞特大學 的研究小組指出,印度喀拉拉學校也曾發現可用於計算
圓周率 的無窮級數,並利用它將圓周率的值精確到小數點後第9位和第10位,後來又精確到第17位。研究人員說,一個極有說服力的間接證據是,15世紀,印度人曾經將他們的發現告知造訪印度的精通數學的
耶穌會 傳教士。“無窮級數”可能最終擺到了
牛頓 本人的書桌上。
約瑟夫 是在通讀字跡模糊的印度文字材料時得出這些發現的,他的暢銷著作《孔雀之冠:非歐洲的數學之根》(The Crest of the Peacock: the Non-European Roots of Mathematics)的第3版將刊登此次發現,該書由
普林斯頓大學 出版社負責出版。他說:“
現代數學 的起源通常被視為歐洲人取得的一項成就,但中世紀(14至16世紀)印度的這些發現卻被人們忽視或者遺忘了。17世紀末期,牛頓的工作取得了輝煌的成就。他所做的貢獻是不容人們抹殺的,尤其在提到微積分的
運算法則 時更是如此。但
喀拉拉 學校的學者——特別是
馬德 哈瓦(Madhava)和尼拉
坎特 哈(Nilakantha)的名字也同樣不能忘記,他們取得的成就足以和
牛頓 平起平坐,因為正是他們發現了微積分的另一個重要組成部分——無窮級數。”
實用冪級數
約瑟夫 表示:“
喀拉拉 學校所做的貢獻未能獲得世人的承認有很多原因,其中一個最重要的原因便是對非歐洲世界的科學發現漠然視之的態度,這種做法無疑是對歐洲殖民主義在科學領域的一種延續。此外,對於中世紀的喀拉拉語、
馬拉雅拉姆語 等印度當地語言的形態,外人可以說是知之甚少,而諸如《Yuktibhasa》等一些最具有開創性的著作卻又偏偏使用了這些語言。《Yuktibhasa》的大部分篇幅都用來闡述產生重要影響的無窮級數。”他指出:“我們真的無法想像,西方社會能夠拋棄奉行了500年之久的傳統,從印度和伊斯蘭世界‘進口’學識和著作。但我們還是發現了強有力的證據,例如,由於當時的歐洲耶穌會士曾造訪這一地區,所以他們有很多收集相關信息的機會。更為重要的是,這些耶穌會士不但精通數學,同時也精通當地的語言。
約瑟夫 說:“他們之所以這么做實際上有很大的動機:教皇
格雷戈里 八世組建了一個委員會,專門負責為羅馬的儒略曆實現現代化。這個委員會的成員包括德國耶穌會士、天文學家兼數學家克拉維烏斯,他曾多次要求獲得世界其它地區的人如何打造曆法的信息,而
喀拉拉 學校無疑在這一領域扮演著領導者的角色。”他表示:“類似地,人們對更有效的導航方式的需求也變得越發強烈,包括在探險之旅中如何保持時間的準確性。此外,致力於天文學研究的數學家也可憑藉自己的努力獲得大獎。因此,歐洲重要的耶穌會研究人員的足跡便開始遍布全世界,以獲得相關的知識和信息,而喀拉拉學校的數學家無疑是這一領域的大師。王巴S”
記號 此數列構成下列表達式
稱以上表達式為常數項無窮級數 (infinite series ),簡稱級數 ,記為
性質 無窮級數具有以下性質:
1 、級數收斂的一個必要條件是它的通項以0為
極限 。
證:
2 、若有一個無窮級數 :每一項乘以一個
常數 ,則其和等於
。即
3 、收斂級數可以逐項相加或相減,如有兩個無窮級數:
, 4 、級數中去掉或加上或改變有限項不影響其收斂性,
如:
和
這兩個級數的斂散性是一樣的,但極限值不一定相等。
無窮級數 無窮級數 5 、收斂級數的部分和數列
的子數列
也收斂(逆否命題也成立),並且其和就是原級數的和;若
收斂,則
未必收斂。
6、 3的推論:如果任意有限個無窮級數都是收斂的,那么它們任意的
線性組合 也必定是收斂的。注意對於都是發散的級數,則不存在類似的結論。
7、 5的推論:若級數 收斂,則
收斂,其所對應的新的級數(通項:
)必收斂(逆否命題也成立);若僅
收斂,則級數未必收斂。
無窮級數 冪級數 一個任意項級數,如果由它的各項的絕對值所得到的級數收斂,則原來的級數也收斂,如果發散,則原來的級數不一定也發散,如果反而是收斂,則稱這種級數為條件收斂的。實際上,
條件收斂 的級數,可以通過變換級數各項的順序而使得這個級數收斂於任意
實數 ,也能發散至無窮大。
收斂半徑和收斂區間
級數的每一項也可以是函式,這種級數稱為函
數項級數 。
這裡我們討論一種特定的函式項級數,即由如下形式的冪函式組成的級數,稱為冪級數。
也可以直接寫成。冪級數的斂散性具有很好的特徵,即所謂
阿貝爾定理 :如果冪級數在點x=k處收斂,那么它在
區間 內的每一點處都
絕對收斂 ;反之,如果冪級數在點x=k 處發散,那么對於不屬於的所有x都發散。上面的定理使得
冪函式 的收斂域只能是一個開區間,稱為冪級數的收斂區間。收斂區間的長度的一半稱為
收斂半徑 。套用對於正項級數的比值判別法和根值判別法的
極限 形式,可以求出冪級數的收斂半徑。
設對於冪級數
的係數,有
,其中
為有限數值或者是無窮大。進一步使
,利用
根值審斂法 ,就有如下結果:
⑴ 如果
,則在
時,冪級數絕對收斂,而
時,冪級數發散。因此,此時冪級數的收斂半徑為
。
⑵ 如果
,則對於任意的x,冪級數都是絕對收斂的。因為此時
,小於1。這時可以認為冪級數的收斂半徑為無窮大。
無窮級數 ⑶ 如果
為無窮大,則冪級數只在x=0處收斂,而取任意非零的數值時,級數都是發散的,因此可以認為冪級數的收斂半徑為0。
對於形如
的冪級數,類似地,也可以根據根值判別法的
極限 形式,得到相同的結論。求出冪級數的收斂半徑以後,即可得到相應的收斂
區間 和收斂區域。
無窮級數 冪級數的微分、積分、連續性
對於一個
冪級數 ,如果它的收斂半徑大於0,那么在它的收斂區域內,就得到了一個確定的以這個收斂區域為
定義域 的函式,為這個冪級數的和函式,自然,對於這個和函式也應該能夠套用
微積分 的方法加以研究。
無窮級數 如果冪級數
的收斂半徑r大於0,則它的和函式S(x)在(-r,r)上必定可積,並且導函式為
。和函式的
可微 區間 是開區間,因為即使和函式在這個區間的
端點 可能有定義,這個定理也不能保證和函式在端點處具有可微性。
無窮級數 和函式還具有
連續性 :如果冪級數的收斂半徑r大於0,則它的和函式S(x)在其定義域上連續。對於連續性,定理強調的是在它的定義域上,也就是包括有定義的端點。連續性也就意味著可以對
冪級數 逐項求極限。
無窮級數 展開式 冪級數展開式 無窮級數 實用冪級數 無窮級數 傅立葉級數 三角級數 洛朗級數 泰勒級數是洛朗級數的特殊形式。
發散性質 首先我們只是考慮級數的斂散性的問題,也就是存在性問題,而不是如何求
極限 的問題。關於無窮級數的斂散性,有如下的基本性質:
任意改變一個級數的任意有限個項的值,都不影響這個級數的斂散性。原因很顯然,只要對一個
級數 所作的改變是有限的,就不能使得這個級數,由趨向於無窮而變得趨向於有限,也不能使得這個級數由趨向於有限而變得趨向於無窮,或者是由根本不存在任何極限,而變得出現極限。
判別法 正項級數及其斂散性
如果一個無窮級數的每一項都大於或等於0,則這個級數就是所謂的正項級數。
正項級數 的主要特徵就是如果考慮級數的部分和
數列 ,就得到了一個單調上升數列。而對於單調上升數列是很容易判斷其斂散性的:
正項級數收斂的充要條件是部分和數列有界。
有界性 可以通過許多途徑來進行判斷,由此我們可以得到一系列的斂散性判別法。
比較 ⑴一個正項級數,如果從某個有限的項以後,所有的項都小於或等於一個已知收斂的級數的相應項,那么這個正項級數也肯定收斂。
⑵反之,一個正項級數,如果從某個有限的項以後,所有的項都大於或等於一個已知發散的級數的相應項,那么這個正項級數也肯定發散。
如果說逐項的比較還有些麻煩的話,可以採用如下的極限形式:對於正項級數和 ,如果 ,即它們的通項的比趨向於一個非0的有限值,那么這兩個級數具有相同的斂散性。
積分 對於正項級數如果存在一個單調下降
連續函式 f(x),有
,那么級數
與
廣義積分 具有相同的斂散性。
比值 設正項級數從一個確定的項以後,每一項都嚴格大於0,並且如果有
,a是某個實數,那么這個級數收斂。反之,如果從一個確定的項以後,每一項都嚴格大於0,並且有
,則級數發散。同樣這種比較也可以採用極限形式:若
,則級數發散;若
,則級數收斂。如果
,則本判別法無法進行判斷。
根值 對於正項級數,如果從某一個確定的項開始,都有
,則級數收斂,反之,如果從任何給定的項之後,都存在一項滿足
,則級數發散。同樣這種比較也可以採用極限形式:設正項級數從一個確定的項以後,
,則級數絕對收斂。若
,則級數發散。若非以上兩者,則本判別法無法進行判斷。
絕對收斂 實際上針對正項級數的斂散性判別法的有效範圍還可以擴大,也就是說,還可以用於判斷更多的級數是收斂的。這是通過引入絕對收斂的概念而得到的。
如果我們把一個任意項的級數的每一項都取絕對值,那么就得到了一個正項級數,如果這個正項級數是收斂的,那么這個任意項級數就被稱為是絕對收斂的。
給出絕對收斂這么一類任意項級數的好處,就在於:
一個級數如果是絕對收斂的,那么也就一定是收斂的。
絕對收斂級數不僅具有可以套用針對正項級數的斂散性的判別法的特性,還具有如下的性質:
如果把任意項級數的所有正項都保持不變,而所有負項都更換為0,那么就得到一個正項級數 ;如果把它的所有負項都改變符號,而正項都更換為0,則得到另一個正項級數 ,然後就得到一個任意項級數的絕對收斂的充要條件,為正項級數與都收斂。從這個性質能夠得到一個推論,即:如果任意項級數絕對收斂,就有。
作為
加法交換律 的一個推廣,對於正項級數,如果任意改變它的各項的相加順序,不會改變它的斂散性,同樣,對於絕對收斂級數也有這樣的性質。
不只是對於加法的交換律,對於絕對收斂級數的乘積也有性質:
如果兩個任意項級數都絕對收斂,那么它們的各項的乘積,按照任意方法排列而得到的級數同樣絕對收斂,並且和為兩個任意項級數的和的乘積。
交錯級數 考慮一種特別的級數形式,即相鄰兩項的符號相反,稱為
交錯級數 。交錯級數具有一個簡單的性質:
如果
為一個單調
遞減數列 ,並且以0為
極限 ,那么通過改變這個數列相鄰兩項的符號而構造的兩個交錯級數都收斂。
這種級數稱為萊布尼茲級數。



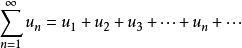


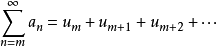






 無窮級數
無窮級數 無窮級數
無窮級數






 無窮級數
無窮級數



 無窮級數
無窮級數


 無窮級數
無窮級數 無窮級數
無窮級數
 無窮級數
無窮級數

 無窮級數
無窮級數





































 無窮級數
無窮級數 無窮級數
無窮級數
 無窮級數
無窮級數