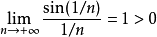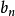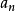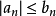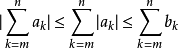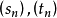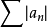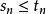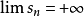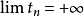基本介紹
- 中文名:比較審斂法
- 外文名:Comparison test、Direct comparison test
- 別名:比較審斂原理
定理,證明,推論,典型題,
定理
(1)若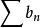 收斂,則
收斂,則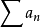 收斂。
收斂。
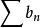
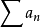
(2)若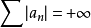 ,則級數
,則級數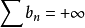 。
。
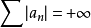
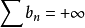
證明
推論
(1)如果級數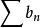 收斂,且存在正整數N,使當
收斂,且存在正整數N,使當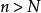 時,(k>0)成立,則級數
時,(k>0)成立,則級數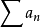 收斂;
收斂;
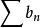
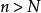
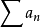
(2)如果級數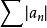 發散,且存在正整數N,使當
發散,且存在正整數N,使當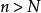 時,(k>0)成立,則級數
時,(k>0)成立,則級數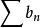 發散。
發散。
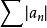
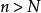
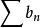
典型題
判斷一般項為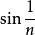 的無窮級數的收斂性:
的無窮級數的收斂性:
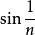
因為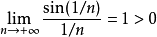 ,而一般項為1/n的級數發散(調和級數發散),由比較審斂法知此級數發散。
,而一般項為1/n的級數發散(調和級數發散),由比較審斂法知此級數發散。