基本介紹
- 中文名:求導
- 外文名:derivation
- 特性:可導的函式一定連續
- 特性:不連續的函式一定不可導
- 套用:物理學、幾何學、經濟學
- 表示:f'(x)
- 對象:因變數的增量
定義

常見求導法則


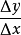



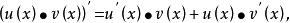





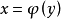






特殊求導法則







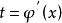
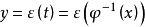





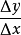



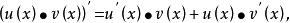





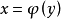













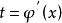
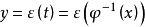

求導是數學計算中的一個計算方法,它的定義就是,當自變數的增量趨於零時,因變數的增量與自變數的增量之商的極限。在一個函式存在導數時,稱這個函式可導或者可微分...
對數求導法是一種求函式導數的方法。取對數的運算可將冪函式、指數函式及冪指函式運算降格成為乘法運算,可將乘法運算或除法運算降格為加法或減法運算,使求導運算計算...
(求導法則中的Leibniz公式)編輯 鎖定 討論999 萊布尼茨法則,也稱為乘積法則,是數學中關於兩個函式的積的導數的一個計算法則。中文名 萊布尼茨公式 外文名 Leibniz...
鏈式法則(英文chain rule)是微積分中的求導法則,用以求一個複合函式的導數。所謂的複合函式,是指以一個函式作為另一個函式的自變數。如設f(x)=3x,g(x)=3x+...
求導去噪是指對光纖探頭採集的LIBS光譜數據進行微分,從而得到新的數據矩陣,其主要的思路是順著光譜數據曲線計算出每個數據點處的斜率,將每個LIBS光譜數據點處的斜率...
由基本函式的和、差、積、商或相互複合構成的函式的導函式則可以通過函式的求導法則來推導。基本的求導法則如下:1、求導的線性:對函式的線性組合求導,等於先對...
對於雙曲函式shx,chx,thx等以及反雙曲函式arshx,archx,arthx等和其他較複雜的複合函式求導時通過查閱導數表和運用開頭的公式與 4.y=u土v,y'=u'...
二階導數,是原函式導數的導數,將原函式進行二次求導。一般的,函式y=f(x)的導數y‘=f’(x)仍然是x的函式,則y’'=f’'(x)的導數叫做函式y=f(x)的二...
不僅如此,萊布尼茲甚至引入(d)x 和 (d)y,稱其為“未消失的量”,用以進行求導前部的計算。在完成計算後再用“消失的量”dx 和dy來代替它們,並假定前兩者之...
對任意n階導數的計算,由於 n 不是確定值,自然不可能通過逐階求導的方法計算。此外,對於固定階導數的計算,當其階數較高時也不可能逐階計算。...
按偏導數的定義,將多元函式關於一個自變數求偏導數時,就將其餘的自變數看成常數,此時他的求導方法與一元函式導數的求法是一樣的。...
如果f(x)在(a,b)內可導,且在區間端點a處的右導數和端點b處的左導數都存在,則稱f(x)在閉區間[a,b]上可導,f'(x)為區間[a,b]上的導函式,簡稱導數。...
複合函式求導的前提:複合函式本身及所含函式都可導。法則1:設u=g(x),對f(u)求導得:f'(x)=f'(u)*g'(x);法則2:設u=g(x),a=p(u),對f(a)求導...
在函式定義域的內點,對某一方向求導得到的導數。一般為二元函式和三元函式的方嚮導數,方嚮導數可分為沿直線方向和沿曲線方向的方嚮導數。...
假設π/2-x=u,我們可以用連鎖律對餘弦函式y=cos x求導:d/dx(cos x)=d/dx[sin (π/2-x)]=d/du[sin (π/2-x)]×d/dx(π/2-x) (連鎖律)...
對於一個已經確定存在且可導的情況下,我們可以用複合函式求導的鏈式法則來進行求導。在方程左右兩邊都對x進行求導,由於y其實是x的一個函式,所以可以直接得到帶有 y...
處不可導。對數導數求導方法 編輯 由導數定義,我們可以得到求函式 在點 處的導數的方法[1] [1] :(1)求函式的增量 ;(2)求平均變化率;(...
鏈式法則是微積分中的求導法則,用於求一個複合函式的導數,是在微積分的求導運算中一種常用的方法。複合函式的導數將是構成複合這有限個函式在相應點的 導數的乘積...
