基本介紹
- 中文名：高階導數
- 外文名：Higher-order derivative
- 學科：數學
- 含義：二階以上的導數
- 方法：萊布尼茲法等
- 相關名詞：二階導數
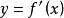
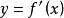
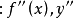
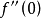
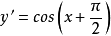
簡介,高階導數的計算法則,任意階導數的計算,常用的高階導數公式,
簡介
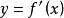
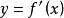
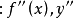
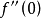
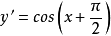
一階導數的導數稱為二階導數，二階以上的導數可由歸納法逐階定義。二階和二階以上的導數統稱為高階導數。從概念上講，高階導數可由一階導數的運算規則逐階計算，但從實際運算考慮這種做法是行不通的。因此有必要研究高階導數特別是任意階導數的計算方法。
或者可以寫成：
類似地，二階導數的導數叫做三階導數，三階導數的導數叫做四階導數…… . 一般地，n-1階導數的導數叫做 n 階導數，即
分別記作
或者寫為
二階及二階以上的導數統稱為高階導數。
從概念上講，高階導數計算就是連續進行一階導數的計算。因此只需根據一階導數計算規則逐階求導就可以了，但從實際計算角度看，卻存在兩個方面的問題：
（1）一是對抽象函式高階導數計算，隨著求導次數的增加，中間變數的出現次數會增多，需注意識別和區分各階求導過程中的中間變數。
（2）二是逐階求導對求導次數不高時是可行的，當求導次數較高或求任意階導數時，逐階求導實際是行
不通的，此時需研究專門的方法。
高階導數的計算法則
從理論上看，逐次套用一階導數的求導規則就可得到高階導數相應的運算規則。然而，對於和、差的導數計算的線性規則，這種推導是方便的，而對乘積求導的非線性運算規則，其推導過程和結果就未必簡單了。
1.
和的n階導數：
設函式 在點x都具有 n 階導數，則有
2. 積的 n 階導數 ─萊布尼茲公式：
設函式 在點x都具有 n 階導數，則由一階導數乘積的運算法則有
這一結果稱為萊布尼茲公式。
例：設
存在，求
分析：這是半抽象複合函式求二階導數問題。由於已知
存在，故只需按導數規則逐階求導即可。
解：
例：已知
，求
。
分析：對此連乘積形式的函式求二階導數，直接按乘乘積求導法則求導顯然比較繁雜，故可考慮將乘積化為和差再按和的求導法則計算。
連續兩次套用和差化積公式有：
由此便容易求得：
於是求得：
任意階導數的計算
對任意n階導數的計算，由於 n 不是確定值，自然不可能通過逐階求導的方法計算。此外，對於固定階導數的計算，當其階數較高時也不可能逐階計算。
所謂n階導數的計算實際就是要設法求出以n為參數的導函式表達式。求n階導數的參數表達式並沒有一般的方法，最常用的方法是，先按導數計算法求出若干階導數，再設法找出其間的規律性，並導出n的參數關係式。
例：設
，求
分析：這是基本初等函式求任意階導數的問題，其求導任務實際是尋求導函式表達式與導數階數 n 的關係。為找出其間的規律性，可先具體計算若干階導數，再設法確定一般規律。
解：用歸納法尋求任意階導函式表達式：
通過若干階導數的計算可看出，cosx的高階導數具有一種循環性，其循環規律涉及兩個因素，一是總在sin x 和 cos x 之間互動轉換，二是符號互動變化。
由於涉及兩個變化因素，使得確定導數規律相對困難，故考慮改寫各階導數形式，以減少其間變化因素，並使其和導數階數發生聯繫。
由此可見，cosx的n階導數可一般地寫成：
類似地可求得：
常用的高階導數公式
