基本介紹
歷史
定義
一般定義
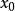
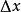


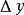









幾何意義




 圖1.幾何意義
圖1.幾何意義性質
 圖2.單調性
圖2.單調性
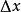


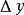













 圖1.幾何意義
圖1.幾何意義 圖2.單調性
圖2.單調性導數(英語:Derivative)是微積分學中重要的基礎概念。一個函式在某一點的導數描述了這個函式在這一點附近的變化率。導數的本質是通過極限的概念對函式進行局部的線性...
導數(Derivative),也叫導函式值。又名微商,是微積分中的重要基礎概念。當函式y=f(x)的自變數x在一點x0上產生一個增量Δx時,函式輸出值的增量Δy與自變數...
一階導數的導數稱為二階導數,二階以上的導數可由歸納法逐階定義。二階和二階以上的導數統稱為高階導數。從概念上講,高階導數可由一階導數的運算規則逐階計算,...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
一階偏微分方程是最簡單的一類偏微分方程。一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的...
導數光譜法亦稱微分光譜,屬紫外吸收光譜派生的一個分支, 由於對複雜組分可不經分離而直接測定,方法簡便、快速、準確,近年來得到迅速發展和廣泛套用。 ...
一階微分形式不變性是指:無論u,v是自變數還是中間變數,函式z=f(u,v)的全微分形式是一樣的。此性質的好處是:一方面是可以不用區分變數直接利用一元函式的微分...
二階導數,是原函式導數的導數,將原函式進行二次求導。一般的,函式y=f(x)的導數y‘=f’(x)仍然是x的函式,則y’=f’(x)的導數叫做函式y=f(x)的二階...
三階導數是由原函式導數的導數的導數。...... 即原函式導數的導數的導數,將原函式進行三次求導,不代表該點的曲率,談幾何意義頂多只能算代表原函式一階導數的凹凸...
形如y'=f(y/x)的一階微分方程,稱為齊次一階微分方程。齊次微分方程是一個微分方程,如果它的一個解乘以任意常數後,仍是它的解,則稱為齊次微分方程。對一階...
一階擬線性偏微分方程(quasi-linear partial differential equation of first order)是一類特殊的一階非線性偏微分方程,關於未知函式的偏導數是線性的一階非線性偏...
在微積分,駐點(Stationary Point)又稱為平穩點、穩定點或臨界點(Critical Point)是函式的一階導數為零,即在“這一點”,函式的輸出值停止增加或減少。對於一維...
利潤極大化的必要條件是π對Q的一階導數為零。而TR對Q的一階導數就是邊際收益MR,同樣,就是邊際成本MC。所以,當MR=MC,即邊際收益等於邊際成本時,利潤極大。...
一元微分又叫常微分。微分高階型 編輯 當自變數是多元變數時,導數的概念已經不適用了(儘管可以定義對某個分量的偏導數),但仍然有微分的概念。微分定義 ...
撓曲線在截面位置坐標x處的斜率,或撓度γ對坐標x的一階導數,等於該截面的轉角。關於撓度和轉角正負符號的規定:在上圖選定的坐標系中,向上的撓度為正,逆時針轉向...
在數學中,差分法(difference methods,簡稱DM),是一種微分方程數值方法,是通過有限差分來近似導數,從而尋求微分方程的近似解。“差分法”是在比較兩個分數大小時,...
光滑函式(smooth function)是指在其定義域內無窮階數連續可導的函式。...若一元函式在閉區間上分段連續,至多除有限個點之外可微且導數連續,在這有限個...
簡單來講,線性微分方程是指關於未知函式及其各階導數都是一次方,否則稱其為非線性微分方程。...
