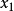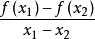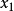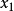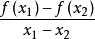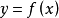定義
函式的單調性(monotonicity)也叫函式的增減性,可以
定性描述在一個指定
區間內,
函式值變化與
自變數變化的關係。當函式
f(
x) 的自變數在其定義區間內增大(或減小)時,函式值也隨著增大(或減小),則稱該函式為在該區間上具有單調性(單調增加或單調減少)。在
集合論中,在
有序集合之間的函式,如果它們保持給定的次序,是具有單調性的。
如果說明一個函式在某個區間D上具有單調性,則我們將D稱作函式的一個單調區間,則可判斷出:
注意:函式單調性是針對某一個區間而言的,是一個局部性質。因此,說單調性時最好指明
區間。
有些函式在整個定義域內是單調的;有些函式在定義域內的部分區間上是增函式,在部分區間上是
減函式;有些函式是非單調函式,如常數函式。
函式的單調性是函式在一個
單調區間上的“整體”性質,具有任意性,不能用特殊值代替。
在利用
導數討論函式的單調區間時,首先要確定
函式的
定義域,解決問題的過程中只能在
定義域內,通過討論導數的符號來判斷函式的單調區間。
單調函式
如果對於屬於定義域
D內某個
區間上的任意兩個
自變數的值x
1,x
2∈D且x
1>x
2,都有
f(x
1) >
f(x
2),即在D上具有單調性且單調增加,那么就說
f(x) 在這個區間上是
增函式。
相反地,如果對於屬於定義域D內某個
區間上的任意兩個
自變數的值x
1,x
2∈D且
x1>x
2,都有f(x
1) <f(x
2),即在D上具有單調性且單調減少,那么就說
f(x) 在這個區間上是
減函式。
性質
圖象性質
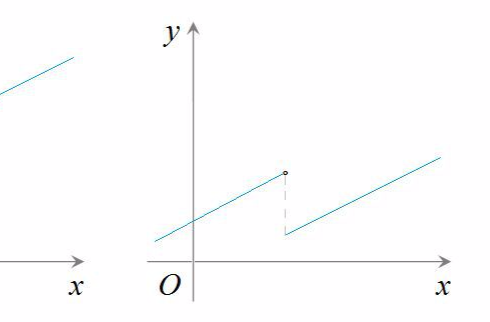
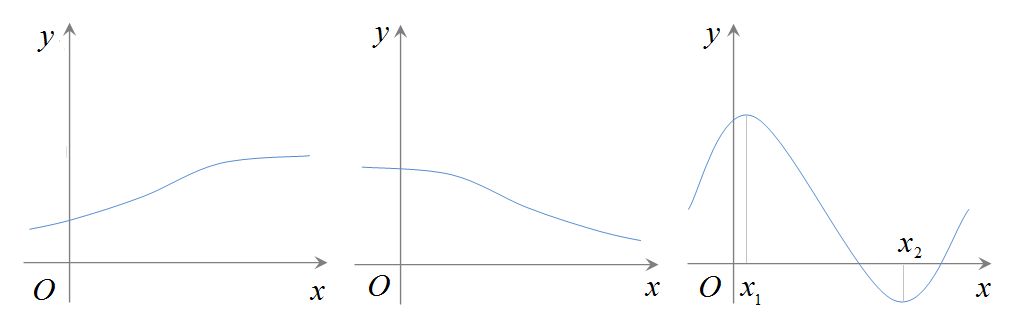 函式圖象
函式圖象函式單調性的幾何特徵:在單調區間上,增函式的圖象是上升的,減函式的圖象是下降的。
當x1 < x2時,都有f(x1)<f(x2) 等價於 ;
當x1 < x2時,都有f(x1)>f(x2) 。
如上圖右所示,對於該特殊函式f(x),我們不說它是增函式或減函式,但我們可以說它在區間 [x1,x2]上具有單調性。
運算性質
f(x)與f(x)+a具有相同單調性;
f(x)與 g(x) = a·f(x)在 a>0 時有相同單調性,當 a<0 時,具有相反單調性;
當f(x)、g(x)都是增(減)函式時,若兩者都恆大於零,則f(x)×g(x)為增(減)函式;若兩者都恆小於零,則為減(增)函式;
兩個增函式之和仍為增函式;增函式減去減函式為增函式;兩個減函式之和仍為減函式;減函式減去增函式為減函式;函式值在區間內同號時, 增(減)函式的倒數為減(增)函式。
判斷方法
1、圖象觀察法
如上所述,在單調區間上,增函式的圖象是上升的,減函式的圖象是下降的。因此,在某一區間內,一直上升的函式
圖象對應的函式在該
區間單調遞增;
一直下降的函式圖象對應的函式在該區間單調遞減;
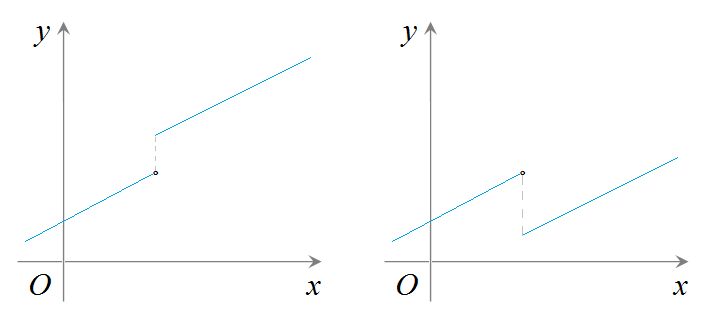 兩個分段函式
兩個分段函式注意:對於
分段函式,要特別注意。例如,上圖左可以說是一個
增函式;上圖右就不能說是在
定義域上的一個增函式(在定義域上不具有單調性)。
2、定義法
根據函式單調性的定義,在這裡只闡述用定義證明的幾個步驟:
③對
的結果進行變形處理(通常是配方、因式分解、有理化、通分,利用公式等等);
⑤下結論,根據“同增異減”原則,指出函式在區間上的單調性。
3、等價定義法
設函式
的定義域為D,在定義域內任取
,
,且
,若
>0,則函式單調遞增;若有 <0,則函式單調遞減(證明從略),以上是函式單調性的第二定義。
4、求導法
導數與函式單調性密切相關。它是研究函式的另一種方法,為其開闢了許多新途徑。特別是對於具體函式,利用導數求解函式單調性,思路清晰,步驟明確,既快捷又易於掌握,利用導數求解函式單調性,要求熟練掌握基本求導公式。
如果函式y=f(x)在區間D內可導(可微),若x∈D時恆有f'(x)>0,則函式y=f(x)在區間D內單調增加;反之,若x∈D時,f'(x)<0,則稱函式y=f(x)在區間D內單調減少。
5、複合函式法
在函式y=f[g(x)]的定義域內,令u=g(x),則y=f[g(x)]的單調性由u=g(x)與y=f(x)的單調性共同確定,方法如下
u=g(x) | y=f(x) | y=f[g(x)] |
增函式 | 增函式 | 增函式 |
減函式 | 減函式 | 增函式 |
增函式 | 減函式 | 減函式 |
減函式 | 增函式 | 減函式 |
因此,複合函式的單調性可用“同增異減”來判定,但要考慮某些特殊函式的定義域。
註:y=f(x)+g(x)不屬於
複合函式,因此不在此方法的適用範圍內。
套用
利用函式單調性可以解決很多與函式相關的問題。通過對函式的單調性的研究,有助於加深對函式知識的把握和深化,將一些實際問題轉化為利用函式的單調性來處理。因此對函式單調性的討論小僅有重要的理論價值,而且具有很好的套用價值。本文結合一些典型例題分析說明函式單調性的套用,如利用函式的單調性求最值、解方程、證明小等式等。
1、利用函式單調性求最值
求函式的最大(小)值有多種方法,但基本的方法是通過函式的單調性來判定,特別是對於小可導的連續點,開區問或無窮區問內最大(小)值的分析,一般都用單調性來判定。
2利用函式單調性解方程
函式單調性是函式一個非常重要的性質,由於單調函式
中x與y是一對應的,這樣我們就可把複雜的方程通過適當變形轉化為型如“
”方程,從而利用函式單調性解方程x=a,使問題化繁為簡,而構造單調函式是解決問題的關鍵。
3、利用函式單調性證明不等式
首先,根據小等式的特點,構造一個單調函式;其次,判別此函式在某區問[a,b]上為單調函式;最後,由單調函式的定義得到我們要證明的小等式。
 函式圖象
函式圖象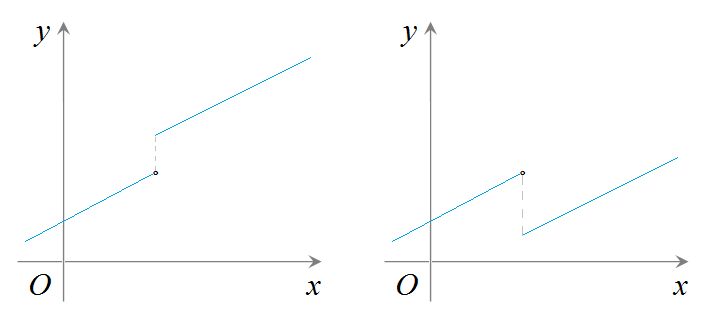 兩個分段函式
兩個分段函式