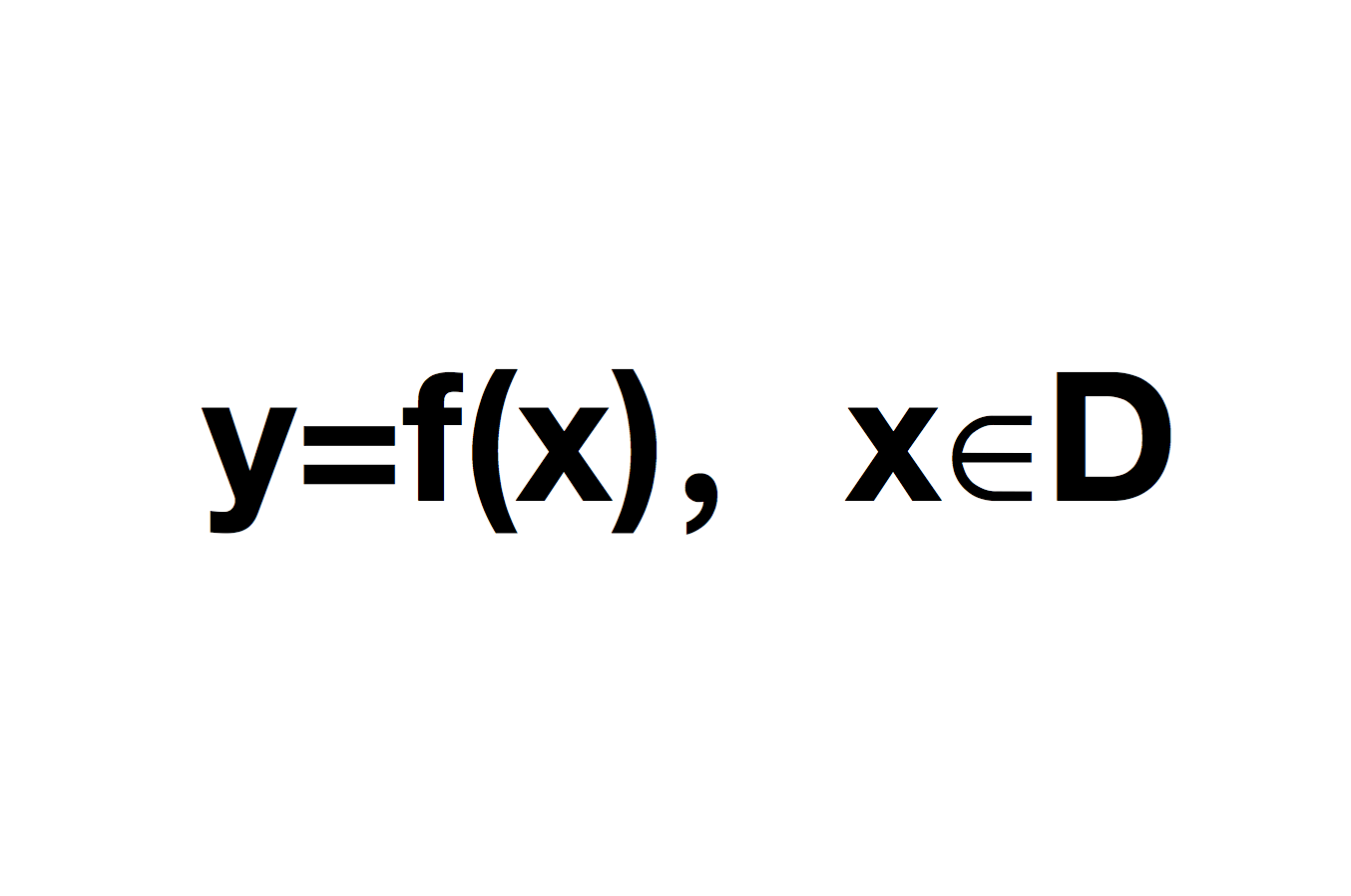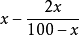基本介紹
- 中文名:定義域
- 外文名:Domain
- 學科:數學物理化學
- 解釋:函式三要素之一
定義,求解類型,類型一,類型二,類型三,類型四,
定義
定義一:設x、y是兩個變數,變數x的變化範圍為D,如果對於每一個數x∈D,變數y遵照一定的法則總有確定的數值與之對應,則稱y是x的函式,記作y=f(x),x∈D,x稱為自變數,y稱為因變數,數集D稱為這個函式的定義域。
1,給定定義域:例如:函式 的定義域為給定的集合{1,2}。
的定義域為給定的集合{1,2}。

3,實際問題:根據具體情況求定義域。
4,當然,也會運用到動力物理學中求變數
求解類型
抽象函式定義域的常見題型有三種:
類型一
已知 的定義域,求
的定義域,求 的定義域.
的定義域.


例1.已知 的定義域為(-1,1),求
的定義域為(-1,1),求 的定義域.
的定義域.


略解:由 有
有


∴ 的定義域為(0,1)
的定義域為(0,1)

類型二
已知 的定義域,求
的定義域,求 的定義域.
的定義域.


例2.已知 的定義域為(0,1),求
的定義域為(0,1),求 的定義域.
的定義域.


解:已知0<x<1
∴-1<2x-1<1
∴ 的定義域為(-1,1)
的定義域為(-1,1)

注意比較例1與例2,加深理解定義域為x的取值範圍的含義。
類型三
已知 的定義域,求
的定義域,求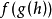 的定義域.
的定義域.

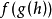
例3.已知 的定義域為(0,1),求
的定義域為(0,1),求 的定義域。
的定義域。


略解:如例2,先求出 的定義域為(-1,1),然後如例1
的定義域為(-1,1),然後如例1

有  ,即
,即


∴ 的定義域為(0,2)
的定義域為(0,2)

指使函式有意義的一切實數所組成的集合。
其主要根據:
①分式的分母不能為零
例4.已知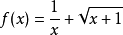 ,求
,求 的定義域。
的定義域。
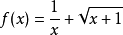

略解: 且
且


∴ 的定義域為
的定義域為


注意:答案一般用區間表示。
例5.已知 ,求
,求 的定義域。
的定義域。


略解:由 有
有


即

∴ 的定義域為(-1,2)
的定義域為(-1,2)

類型四
函式套用題的函式的定義域要根據實際情況來求解。
例6.某工廠統計資料顯示,產品次品率p與日產量x(件)( )的關係符合如下規律:
)的關係符合如下規律:

x | 1 | 2 | 3 | 4 | … | 89 |
p | 2/99 | 1/49 | 2/97 | 1/48 | … | 2/11 |