對數函式

一般地，對數函式以冪（真數）為自變數，指數為因變數，底數為常量的函式。

對數函式是6類基本初等函式之一。其中對數的定義：

如果a^x =N（a>0，且a≠1），那么數x叫做以a為底N的對數，記作x=log_aN，讀作以a為底N的對數，其中a叫做對數的底數，N叫做真數。

一般地，函式y=log_aX（a>0，且a≠1）叫做對數函式，也就是說以冪（真數）為自變數，指數為因變數，底數為常量的函式，叫對數函式。

其中x是自變數，函式的定義域是（0，+∞），即x>0。它實際上就是指數函式的反函式，可表示為x=a^y。因此指數函數裡對於a的規定，同樣適用於對數函式。

“log”是拉丁文logarithm（對數）的縮寫，讀作：[英][lɔɡ][美][lɔɡ, lɑɡ]。

基本介紹

• 中文名：對數函式
• 外文名：Logarithmic Function
• 別稱：對函式
• 表達式：y=logax（a>0 & a≠1）
• 提出者：約翰·納皮爾
• 提出時間：16世紀末
• 套用學科：數學
• 適用領域範圍：解析幾何
• 適用領域範圍：代數學 自然科學
• 函式最值：無
• 函式零點：x=1
• 函式對稱軸：無
• 特點：底大下沉

簡介

對數函式是6類基本初等函式之一。其中對數的定義：

如果a^x=N（a>0，且a≠1），那么數x叫做以a為底N的對數，記作x=log_aN，讀作以a為底N的對數，其中a叫做對數的底數，N叫做真數。

一般地，函式y=log_ax（a>0，且a≠1）叫做對數函式，也就是說以冪（真數）為自變數，指數為因變數，底數為常量的函式，叫對數函式。

其中x是自變數，函式的定義域是（0，+∞），即x>0。它實際上就是指數函式的反函式，可表示為x=a^y。因此指數函數裡對於a的規定，同樣適用於對數函式。

“log”是拉丁文logarithm（對數）的縮寫，讀作：[英][lɔɡ][美][lɔɡ， lɑɡ]。

實際套用

在實數域中，真數式子沒根號那就只要求真數式大於零，如果有根號，要求真數大於零還要保證根號里的式子大於等於零（若為負數，則值為虛數），底數則要大於0且不為1。

對數函式的底數為什麼要大於0且不為1？【在一個普通對數式里 a<0，或=1 的時候是會有相應b的值。但是，根據對數定義：log以a為底a的對數；如果a=1或=0那么log以a為底a的對數就可以等於一切實數（比如log₁1也可以等於2，3，4，5，等等）】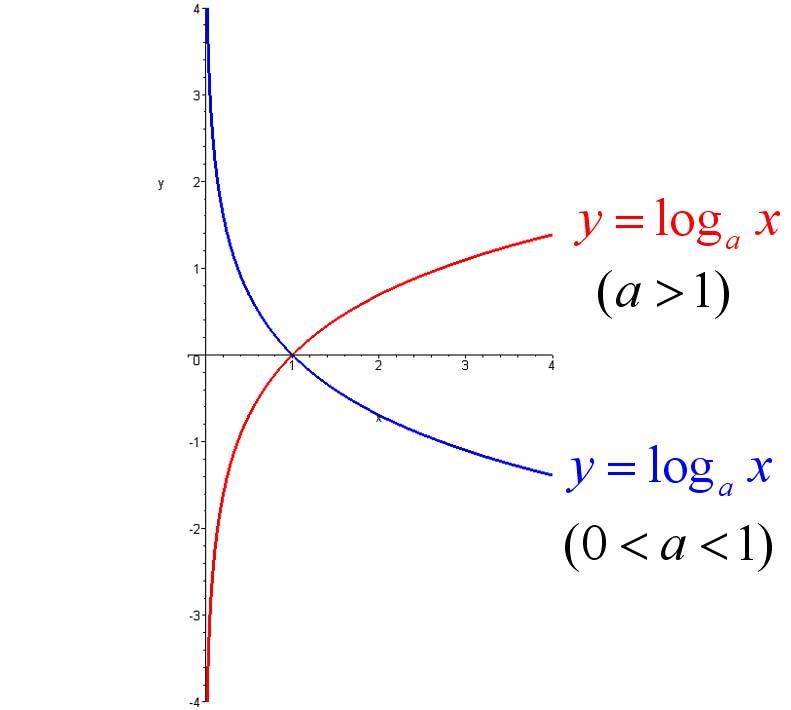

對數函式

通常我們將以10為底的對數叫常用對數（common logarithm），並把log₁₀N記為lgN。另外，在科學計數中常使用以無理數e=2.71828···為底數的對數，以e為底的對數稱為自然對數（natural logarithm），並且把log_eN 記為In N。根據對數的定義，可以得到對數與指數間的關係：

當a>0，a≠1時，a^X=N X=log_aN。（N>0）

由指數函式與對數函式的這個關係，可以得到關於對數的如下結論：

在實數範圍內，負數和零沒有對數；

，log以a為底1的對數為0（a為常數） 恆過點（1，0）。

有理和無理指數

如果 是正整數， 表示等於 的 個因子的加減:

但是，如果是 不等於1的正實數，這個定義可以擴展到在一個域中的任何實數 （參見冪）。類似的，對數函式可以定義於任何正實數。對於不等於1的每個正底數 ，有一個對數函式和一個指數函式，它們互為反函式。

對數可以簡化乘法運算為加法，除法為減法，冪運算為乘法，根運算為除法。所以，在發明電子計算機之前，對數對進行冗長的數值運算是很有用的，它們廣泛的用於天文、工程、航海和測繪等領域中。它們有重要的數學性質而在今天仍在廣泛使用中。

複對數

複對數計算公式

複數的自然對數，實部等於複數的模的自然對數，虛部等於複數的輻角。

產生歷史

16世紀末至17世紀初的時候，當時在自然科學領域（特別是天文學）的發展上經常遇到大量精密而又龐大的數值計算，於是數學家們為了尋求化簡的計算方法而發明了對數。

德國的史蒂非（1487-1567）在1544年所著的《整數算術》中，寫出了兩個數列，左邊是等比數列（叫原數），右邊是一個等差數列（叫原數的代表，或稱指數，德文是Exponent ，有代表之意）。

欲求左邊任兩數的積（商），只要先求出其代表（指數）的和（差），然後再把這個和（差）對向左邊的一個原數，則此原數即為所求之積（商），可惜史提非並未作進一步探索，沒有引入對數的概念。

納皮爾對數值計算頗有研究。他所製造的「納皮爾算籌」，化簡了乘除法運算，其原理就是用加減來代替乘除法。 他發明對數的動機是為尋求球面三角計算的簡便方法，他依據一種非常獨等的與質點運動有關的構想構造出所謂對數方法，其核心思想表現為算術數列與幾何數列之間的聯繫。在他的1619年發表《奇妙的對數表的描述》中闡明了對數原理，後人稱為 納皮爾對數，記為Nap．㏒x，它與自然對數的關係為：

對數的圖像

Nap．㏒x=10㏑（107/x）

由此可知，納皮爾對數既不是自然對數，也不是常用對數，與現今的對數有一定的距離。

瑞士的彪奇（1552-1632）也獨立地發現了對數，可能比納皮爾較早，但發表較遲（1620）。

英國的布里格斯在1624年創造了常用對數。

1619年，倫敦斯彼得所著的《新對數》使對數與自然對數更接近（以e=2.71828...為底）。

對數的發明為當時社會的發展起了重要的影響，簡化了行星軌道運算問題。正如科學家伽利略（1564-1642）說：「給我時間，空間和對數，我可以創造出一個宇宙」。 又如十八世紀數學家拉普拉斯（ 1749-1827）亦提到：「對數用縮短計算的時間來使天文學家的壽命加倍」。

最早傳入我國的對數著作是《比例與對數》，它是由波蘭的穆尼斯（1611-1656）和我國的薛鳳祚在17世紀中葉合 編而成的。當時在lg2=0.3010中，2叫真數，0.3010叫做假數，真數與假數對列成表，故稱對數表。後來改用假數為對數」。

我國清代的數學家戴煦（1805-1860）發展了多種求對數的捷法，著有《對數簡法》（1845）、《續對數簡法》（1846）等。1854年，英國的數學家艾約瑟（1825-1905）看到這些著作後，大為嘆服。

當今中學數學教科書是先講「指數」，後以反函式形式引出「對數」的概念。但在歷史上，恰恰相反，對數概念不是來自指數，因為當時尚無分指數及無理指數的明確概念。布里格斯曾向納皮爾提出用冪指數表示對數的建議。1742年，J．威廉（1675-1749）在給G.威廉的《對數表》所寫的前言中作出指數可定義對數。而歐拉在他的名著《無窮小分析尋論》（1748）中明確提出對數函式是指數函式的逆函式，和21世紀的教科書中的提法一致。

函式性質

定義域求解：對數函式y=log_ax 的定義域是{x 丨x>0}，但如果遇到對數型複合函式的定義域的求解，除了要注意大於0以外，還應注意底數大於0且不等於1，如求函式y=log_x（2x-1）的定義域，需同時滿足x>0且x≠1

和2x-1>0 ，得到x>1/2且x≠1，即其定義域為 {x 丨x>1/2且x≠1}

值域：實數集R，顯然對數函式無界；

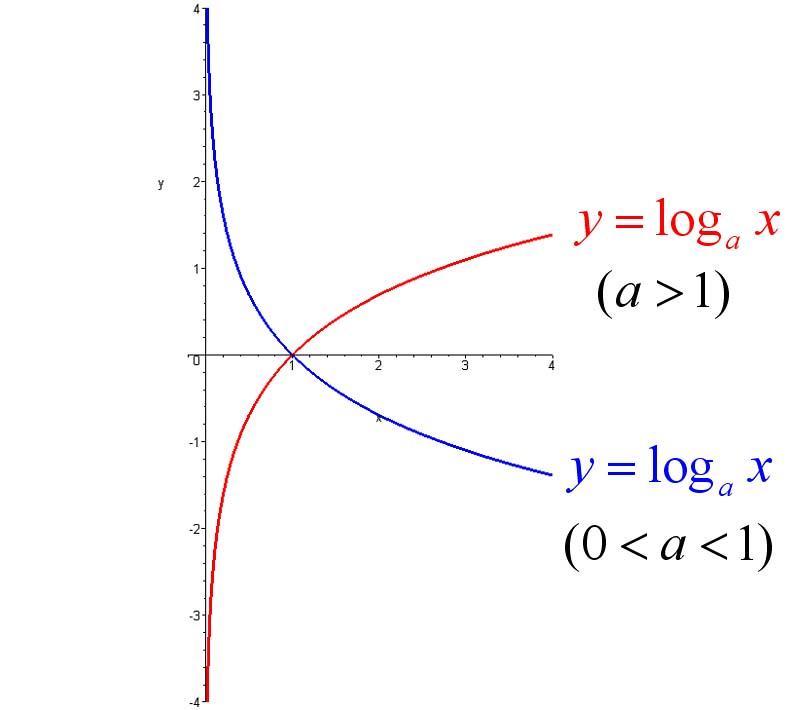
定點：對數函式的函式圖像恆過定點（1，0）；

單調性：a>1時，在定義域上為單調增函式；

0<a<1時，在定義域上為單調減函式；

奇偶性：非奇非偶函式

周期性：不是周期函式

對稱性：無

最值：無

零點：x=1

注意：負數和0沒有對數。

兩句經典話：底真同對數正，底真異對數負。解釋如下：

也就是說：若y=log_ab （其中a>0，a≠1，b>0）

當0<a<1， 0<b<1時，y=log_ab>0;

當a>1， b>1時，y=log_ab>0;

當0<a<1， b>1時，y=log_ab<0;

當a>1， 0<b<1時，y=log_ab<0。

公式推導

e的定義：

設a>0，a≠1

方法一：

指數函式

特殊地，當 時， 。

方法二：

設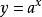 ，兩邊取對數ln y=xln a

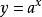
兩邊對x求導：y'/y=ln a，y'=yln a=a^xln a

特殊地，當a=e時，y'=（a^x）'=（e^x）'=e^xln e=e^x。

eº=1

運算性質

性質

一般地，如果a（a>0，且a≠1）的b次冪等於N，那么數b叫做以a為底N的對數，記作log_aN=b，其中a叫做對數的底數，N叫做真數。

底數則要>0且≠1 真數>0

並且，在比較兩個函式值時：

如果底數一樣，真數越大，函式值越大。（a>1時）

如果底數一樣，真數越小，函式值越大。（0<a<1時）

當a>0且a≠1時，M>0，N>0，那么：

對數函式化簡問題

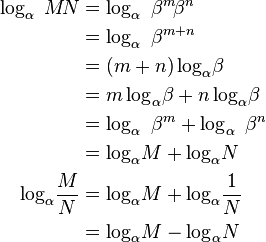和差

和差

換底公式

推導：設

所以

兩邊取對數，則有

即

又因為

所以

指系

互換

倒數

鏈式

表達方式

（1）常用對數：lg（b）=log₁₀b（10為底數）。

（2）自然對數：ln（b）=log_eb（e為底數）。

e為無限不循環小數，通常情況下只取e=2.71828。

與指數的關係

同底的對數函式與指數函式互為反函式。

當a>0且a≠1時，a^x=N x=㏒_aN。

關於y=x對稱。

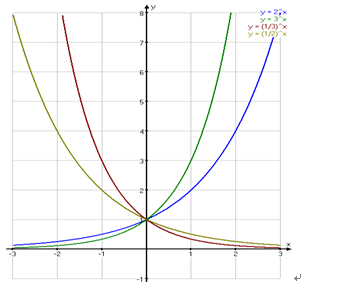
對數函式的一般形式為 y=㏒_ax，它實際上就是指數函式的反函式（圖象關於直線y=x對稱的兩函式互為反函式），可表示為x=a^y。因此指數函數裡對於a的規定（a>0且a≠1），右圖給出對於不同大小a所表示的函式圖形：關於X軸對稱、當a>1時，a越大，圖像越靠近x軸、當0<a<1時，a越小，圖像越靠近x軸。

可以看到，對數函式的圖形只不過是指數函式的圖形的關於直線y=x的對稱圖形，因為它們互為反函式。