基本介紹
直線方程
平面方程





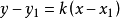



















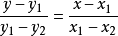


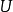





空間方程


有關內容
“角”
距離
套用
點與直線




直線相交點
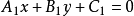





相交直線夾角






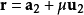






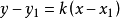



















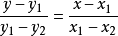


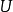











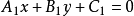











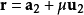

直線由無數個點構成。直線是面的組成成分,並繼而組成體。沒有端點,向兩端無限延長,長度無法度量。直線是軸對稱圖形。它有無數條對稱軸,其中一條是它本身,還有...
從平面解析幾何的角度來看,平面上的直線就是由平面直角坐標系中的一個二元一次方程所表示的圖形。求兩條直線的交點,只需把這兩個二元一次方程聯立求解,當這個...
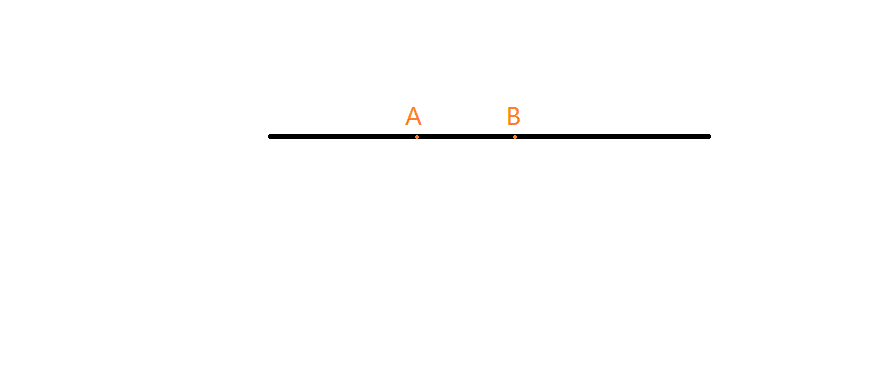
斜率,亦稱“角係數”,表示一條直線相對於橫軸的傾斜程度。一條直線與某平面直角坐標系橫軸正半軸方向的夾角的正切值即該直線相對於該坐標系的斜率。 如果直線與x...
直線系(system of straight lines)亦稱直線束,是具有某一共同性質的直線的集合。如在平面仿射坐標系中,與已知直線Ax+By+C=0平行的所有直線組成一個直線系,它的...
直線形(rectilinear figure)是一類簡單的幾何圖形,指由直線、射線、線段組成的圖形,直線形常把它所劃分的內部區域包括在內。...
直線度公差指單一實際直線允許的變動全量。用於控制平面或空間直線的形狀誤差,其公差帶根據不同的情況有幾種不同的形式。...
對三個投影面無平行、垂直關係,而對三個投影面都傾斜的直線稱為一般位置直線。直線與H,V,W三個投影面的夾角一般分別用α,β,γ表示。一般位置直線的各投影與...
直線一般式方程適用於所有的二維空間直線。它的基本形式是Ax+By+C=0 (A,B不全為零)。因為這樣的特點特別適合在計算機領域直線相關計算中用來描述直線。...
運動物體通過的路徑叫做物體的運動軌跡。運動軌跡是一條直線的運動,叫做直線運動。...... 礎,按其受力的不同可分:勻速直線運動;勻變速直線運動(包括勻加速或勻減...
直線滑台是一種能提供直線運動的機械結構,可臥式或者立式使用,也可以組合成特定的運動機構使用——即自動化行業中通常稱為XY軸、XYZ軸等多軸向運動機構。...
直線型組織結構(linear structure是工業發展初期的一種簡單的組織結構形式。適用於小型組織或現場作業。其特點是組織中的一切管理工作均由領導者直接指揮和管理,不設...
直線行駛是指駕車新手學員駕駛車輛起步,經逐步加速將排檔從最低檔逐檔加到最高檔,使車速達到高速。...
金屬直線軸承是一種以低成本生產的直線運動系統,用於無限行程與圓柱軸配合使用。廣泛套用於精密工具機、紡織機械、食品包裝機械、印刷機械等工業機械的滑動部件。...
直線職權是指組織內直線管理系統的管理人員所擁有的包括發布命令及執行決策等的權力,也就是通常所指的指揮權。直線主管(linemanager)指能指導、監督、指揮、管理下屬...
對於任意一條直線,它可以指示兩個相反的方向,取其中的一個方向叫做它的正方向,這種確定了正方向的直線叫做有向直線,又叫做軸。...
提到回歸直線,首先要知道變數的相關性。變數與變數之間的關係常見的有兩類:一類是確定性的函式關係,像正方形的邊長a和面積S的關係;另一類是變數間確實存在關係,但...
直線運動機構是使構件上某點作準確或近似直線運動的機構。17世紀晚期,在人類能造出精確滑桿和導槽之前出現了一種機械設計思想,目的是用製造簡便的剛片,連桿和鉸...
回歸直線方程指在一組具有相關關係的變數的數據(x與Y)間,一條最好地反映x與y之間的關係直線。離差作為表示Xi對應的回歸直線縱坐標y與觀察值Yi的差,其幾何意義...
過兩點的連線即為一條直線,一般用Ax+By+C=0 (其中A、B不同時為0)來表示。...... 過兩點的連線即為一條直線,一般用Ax+By+C=0 (其中A、B不同時為0)來...
直線塔是輸電線路最常用的一種塔型,也叫過線塔。在輸電線路中直線塔一般用來承受導線的重力,即垂直荷載。...
光在同種均勻介質中沿直線傳播,通常簡稱直線傳播。它是幾何光學的重要基礎,利用它可以簡明地解決成像問題。人眼就是根據光的直線傳播來確定物體或像的位置的,這是...
直線制是最早且最簡單的組織形式,又稱軍隊組織形式,它是企業各級行政單位從上到下實行垂直領導,沒有職能機構。...
直線導軌(linear slider)可分為:滾輪直線導軌,圓柱直線導軌,滾珠直線導軌,三種,是用來支撐和引導運動部件,按給定的方向做往復直線運動。依按摩擦性質而定,直線運動...
直線式:即二次打孔。因孔針排列呈一條直線,故稱直線式。 ...... 直線式:即二次打孔。因孔針排列呈一條直線,故稱直線式。 [1] 參考資料 1. 翟寬編著,新...
直線電機是一種將電能直接轉換成直線運動機械能,而不需要任何中間轉換機構的傳動裝置。它可以看成是一台旋轉電機按徑向剖開,並展成平面而成。直線電機也稱線性電機,...
