基本介紹
- 中文名:點
- 外文名:Point
- 通用學科:科學、數學、哲學
- 通用領域:幾何學、拓撲學、分形、矢量圖形
- 拼音:diǎn
定義無效,點的含義,點的歷史,特殊的點,點的性質,點到點的距離,位置關係,點和點,點和直線,點和平面,點的平移,點的對稱,點的旋轉,其他的點,錯誤理解,
定義無效
在科學系統中總是要對概念下定義,而且一定會用一些已知的概念來定義新的概念,但概念的個數是有限的,又由第二條規則可知,下定義是不能惡性循環的,因此總有一些概念不能引用別的概念來定義,這樣概念叫做這個科學體系中的原始概念。
比如,把平行四邊形定義為兩組對邊分別平行的四邊形,因此就必須先對四邊形、平行以及對邊進行定義。定義四邊形時,應先對多邊形及邊進行定義,又必須先定義折線,故必須先要對點和直線進行定義。但是,在一般的初等幾何中,點和直線都無法再用已被定義過的概念進行定義,它們都是原始概念。在數學中,點、直線、平面、集合,空間、數、量等都是原始概念,但在其中有些是通過公理來直接描述的,雖然有些概念在中學課本中也有解釋,但這種解釋並不是定義。
點的含義
在幾何學、拓撲學以及數學的相關分支中,空間中的點用於描述給定空間中的 1 種特別的對象,在空間中有類似於體積、面積、長、寬、高的類似物。1 個點是 1 個 0 維的對象。點作為最簡單的圖形概念,通常作為幾何學、物理學、矢量圖形和其他領域中最基本的組成部分。
點的歷史
在亞里斯多德的著作【論天體】第三冊中,已經提到數學中的點是沒有大小的,他依此來駁斥柏拉圖將數學的幾何形視為物理實體的構成要素(參見正多面體),並強調這與當時的數學定義相違背:數學的平面沒有厚度,所以不能構造物理實體。他論述說,如果數學平面有厚度,那么數學的線就要有寬度才能夠構成平面,而數學的點必須有大小才能構成線,但是在數學中已經明確定義數學的點是沒有大小的,因此柏拉圖的理論與數學相牴觸。從這裡,亞里斯多德陳述說,一個幾何物件只能分割成相同型態的幾何物件(而不會變成其它的東西):平面只能分割成平面,而不能分割成線;線只能分割成線,不能分割成點;這樣的分割可以無限的進行,而不是像原子論者所說的,最後分割到原子(或是基本構成要素)就停止了。
因此,早在歐幾里得的【幾何原本】之前,數學中的點只用來標示位置的用法已經是共識。亞里斯多德提到點的時候,用的字是 στιγμὰς,是可見的點(spot),而歐幾里得則(小心翼翼的)採用另一個字 σημεῖόν,原意是“標示”(sign):
σημεῖόν ἐστιν, οὗ μέρος οὐθέν.
這句話的意思是:點是沒有部分(μέρος)的東西。點沒有部分,所以也就沒有大小。這個論點來源自亞里斯多德的“部分-整體”理論(part–whole theory):
"the parts are causes of the whole"(整體是由部分所構成的。)
【幾何原本】的阿拉伯文版,將 σημεῖόν 翻譯為 نقطة,意思回到亞里斯多德的可見點;拉丁文版則將 σημεῖόν 翻譯為 punctum,意思是被尖物刺成的小洞。
特殊的點
(內容待補充)
端點:1 條線段兩端上的點或1條射線一端上的點(即線段或射線的起點或終點);

等分點:把 1 條線段平均分成若干條線段的點;
頂點:圖形的邊的公共點;
交點:兩條直線的公共點。
點的性質
- 不可定義性:定義無效;
- 確定性:任意 1 個點都可以用有序數對精確地定位;
- 唯一性:1 組有序數對能且只能定位 1 個點;
- 互異性:任意兩個點都是不同的對象。
點到點的距離
點 A(x,y,z)到點 B(x2,y2,z2)的距離為

位置關係
點和點
- 點和點重合;
- 點和點不重合。

點和直線
- 點在直線上;
- 點在直線外。

點和平面
- 點在平面上;
- 點在平面外。

點的平移
點左右平移只影響橫坐標的變化,點上下平移只影響縱坐標的變化:
設點A的坐標為(x,y).
1若把點A向左平移k(k>0)個單位後,坐標變為(x-k,y);若把點A向右平移k個單位後,坐標則變為(x+k,y).
2.若把點A向上平移k(k>0)個單位後,坐標變為(x,y+k);若把點A向下平移k個單位後,坐標則變為(x,y-k).
3.若把點A先向左平移p個單位,再向上平移q個單位,坐標則變為(x-p,y+q).

點的對稱

點 A(x,y,z)關於點 B(x2,y2,z2)的對稱點的坐標


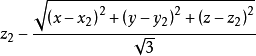
點的旋轉
(內容待補充)

點 A(x,y,z)繞原點旋轉 n°後的位置特徵:
點 A(x,y,z)繞點 B(x2,y2,z2)旋轉 n°後的位置特徵:
其他的點
錯誤理解
線段是由無限個點構成的,而線段的長度讓人們錯誤的認為點是有長度或者長度是無窮小。但這是嚴重錯誤的。因為這違背了測度論和點的基本屬性。點的長度是 0 而不是無窮小。

