基本介紹
- 中文名:集合
- 外文名:aggregate
- 簡稱:集
- 定義:一個或多個確定元素所構成的整體
- 提出者:康托爾
- 創立時間:19世紀
定義
概念
基數
表示
地位
特性
確定性
互異性
無序性
分類
空集
- 空集∅是任意一個非空集合的真子集。
- 空集是任何一個集合的子集。
子集
交並集
 圖1 交集與並集
圖1 交集與並集補集
冪集
區間
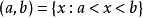

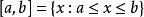





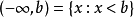



模糊集
相等集合

表示方法
列舉法


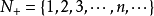

描述法
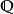



圖像法
符號法
 圖2韋恩圖集合表示法
圖2韋恩圖集合表示法
 圖1 交集與並集
圖1 交集與並集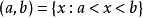

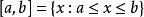





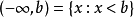






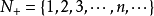

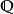



 圖2韋恩圖集合表示法
圖2韋恩圖集合表示法集合,簡稱集,是數學中一個基本概念,也是集合論的主要研究對象。集合論的基本理論創立於19世紀,關於集合的最簡單的說法就是在樸素集合論(最原始的集合論)中的定義...
集合概念是與非集合概念相對的,反映由同類分子有機構成的集合體的概念。如:“中國共產黨”、“森林”。在某一思維對象領域,思維對象可以有兩種不同的存在方式。另...
集合運算是數學科學中常用的詞語,是一種非常有效的構造形體的方法,可以直觀的減少運算難度。...
集合,分散的人或事物聚集到一起,使聚集,緊急集合。... 集合是具有某種特定性質的事物的總體。 這裡的“事物”可以是人,物品,也可以是數學元素。例如: 1、分散的...
數學集合在數學上是一個基礎概念。基礎概念是不能用其他概念加以定義的概念,也是不能被其他概念定義的概念。集合的概念,可通過直觀、公理的方法來下“定義”。集合...
集合類存放於java.util包中。集合類存放的都是對象的引用,而非對象本身,出於表達上的便利,我們稱集合中的對象就是指集合中對象的引用(reference)。集合類型主要有...
計算機科學中,集合是一組可變數量的數據項(也可能是0個)的組合,這些數據項可能共享某些特徵,需要以某種操作方式一起進行操作。一般來講,這些數據項的類型是相同的...
無限集合(infinite set)亦稱無窮集合,是一類特殊的集合,它有下面幾種定義:1.不是有限集的集合;2.可與其真子集對等的非空集合;3.既不是空集,又不與Mn={1,...
集合是指具有某種特定性質的具體的或抽象的對象匯總成的集體,這些對象稱為該集合的元素,數集指就是數的集合。...
模糊集合是用來表達模糊性概念的集合。 又稱模糊集、模糊子集。普通的集合是指具有某種屬性的對象的全體。1965年美國學者扎德在數學上創立了一種描述模糊現象的方法...
集合競價是指對一段時間內接收的買賣申報一次性集中撮合的競價方式。以我國競價交易制度為例,集合競價時成交價格的確定原則是: 1、在有效價格範圍內選取成交量最大...
緊急集合是在緊急情況下迅速進行的集合,是應對突然情況的一種緊急行動。指軍隊、警察或其他準軍事化組織在非常規狀態下或演習情形下突然實行集合。通常以警報,哨聲等...
空集是指不含任何元素的集合。空集是任何集合的子集,是任何非空集合的真子集。空集不是無;它是內部沒有元素的集合。可以將集合想像成一個裝有元素的袋子,而...
集合理財也叫券商集合理財屬於資產管理業務的一種形式,顧名思義,它是券商把社會上零散的資金集中起來,由專家進行管理。它和證券投資基金一樣,都屬於資產管理業務...
集合債券亦稱 “聯合債券”,由兩個或兩個以上的公司聯合發行的債券。集合債券是股份公司為籌措長期資金而發行的債券,發行集合債券是由兩個以上公司的信譽保證的,...
數學的一個基本的分支學科,研究對象是一般集合。集合論在數學中占有一個獨特的地位,它的基本概念已滲透到數學的所有領域。集合論或集論是研究集合(由一堆抽象物件...
集合資產管理計畫:顧名思義是集合客戶的資產,由專業的投資者(券商/基金子公司)進行管理。它是證券公司/基金子公司針對高端客戶開發的理財服務創新產品,投資於產品...
集合符號,英文名A collection of symbols,是數學的分支集合的表達符號,主要套用於計算機領域。...
朱利亞集合是一個在複平面上形成分形的點的集合。以法國數學家加斯頓·朱利亞(Gaston Julia)的名字命名。...
集合名詞(英語:Collective noun)是語言學上的一個專有名詞,意指一種可用來指稱一群對象的字,而這些對象,可以是人、動物、或是一群概念等事物。...
股票集合競價是將數筆委託報價或一時段內的全部委託報價集中在一起,根據不高於申買價和不低於申賣價的原則產生一個成交價格,且在這個價格下成交的股票數量最大,...
《圖片集合》是一款運行在Android平台的軟體,軟體版本為1.1。...... 圖片集合編輯 鎖定 《圖片集合》是一款運行在Android平台的軟體,軟體版本為1.1。...
集合理財產品屬於資產管理方法的一種,顧名思義,它是券商把社會上零散的資金集中起來,由專家進行管理。它和證券投資基金一樣,都屬於資產管理型產品。...
從弗雷格的表述可以看出,集合論悖論涉及到概念結構系統里上下兩級類概念:一是“不屬於自身的類”,一是“不屬於自身的那些類構成的類”。同時也涉及到集合概念。而...
集合資產管理業務是指證券公司設立集合資產管理計畫,與客戶簽訂集合資產管理契約,將客戶資產交由具有客戶交易結算資金法人存管業務資格的商業銀行或者中國證監會認可的...
補集一般指絕對補集,即一般地,設S是一個集合,A是S的一個子集,由S中所有不屬於A的元素組成的集合,叫做子集A在S中的絕對補集。在集合論和數學的其他分支中,...
