數學集合在數學上是一個基礎概念。基礎概念是不能用其他概念加以定義的概念,也是不能被其他概念定義的概念。集合的概念,可通過直觀、公理的方法來下“定義”。
集合(簡稱集)是數學中一個基本概念,它是集合論的研究對象,集合論的基本理論直到19世紀才被創立。最簡單的說法,即是在最原始的集合論——樸素集合論中的定義,集合就是“一堆東西”。集合里的“東西”,叫作元素。若x是集合A的元素,則記作x∈A。集合是把人們的直觀的或思維中的某些確定的能夠區分的對象匯合在一起,使之成為一個整體(或稱為單體),這一整體就是集合。組成一集合的那些對象稱為這一集合的元素(或簡稱為元)。現代數學還用“公理”來規定集合。最基本公理例如:外延公理:對於任意的集合S1和S2,S1=S2若且唯若對於任意的對象a,都有若a∈S1,則a∈S2;若a∈S2,則a∈S1。無序對集合存在公理:對於任意的對象a與b,都存在一個集合S,使得S恰有兩個元素,一個是對象a,一個是對象b。由外延公理,由它們組成的無序對集合是唯一的,記做{a,b}。 由於a,b是任意兩個對象,它們可以相等,也可以不相等。當a=b時,{a,b},可以記做或,並且稱之為單元集合。空集合存在公理:存在一個集合,它沒有任何元素。
基本介紹
- 中文名:數學集合
- 英文名:mathematical aggregation
歷史地位,概念,基數,基數,冪集,性質,特性,確定性,互異性,無序性,符號表示規則,符號,模糊集,
歷史地位
集合在數學領域具有無可比擬的特殊重要性。集合論的基礎是由德國數學家康托爾在19世紀70年代奠定的,經過一大批卓越的科學家半個世紀的努力,到20世紀20年代已確立了其在現代數學理論體系中的基礎地位,可以說,現代數學各個分支的幾乎所有成果都構築在嚴格的集合理論上。
概念
集合是指具有某種特定性質的具體的或抽象的對象匯總成的集體,這些對象稱為該集合的元素。例如全中國人的集合,它的元素就是每一個中國人。我們通常用大寫字母如A,B,S,T,...表示集合,而用小寫字母如a,b,x,y,...表示集合的元素。若x是集合S的元素,則稱x屬於S,記為x∈S。若y不是集合S的元素,則稱y不屬於S,記為y∉S。
基數
元素與集合的關係:
元素與集合的關係有“屬於”與“不屬於”兩種。
集合的分類:
並集:以屬於A或屬於B的元素為元素的集合稱為A與B的並(集),記作A∪B(或B∪A),讀作“A並B”(或“B並A”),即A∪B={x|x∈A,或x∈B}
例如,全集U={1,2,3,5} A={1,3,5} B={1,2,5} 。
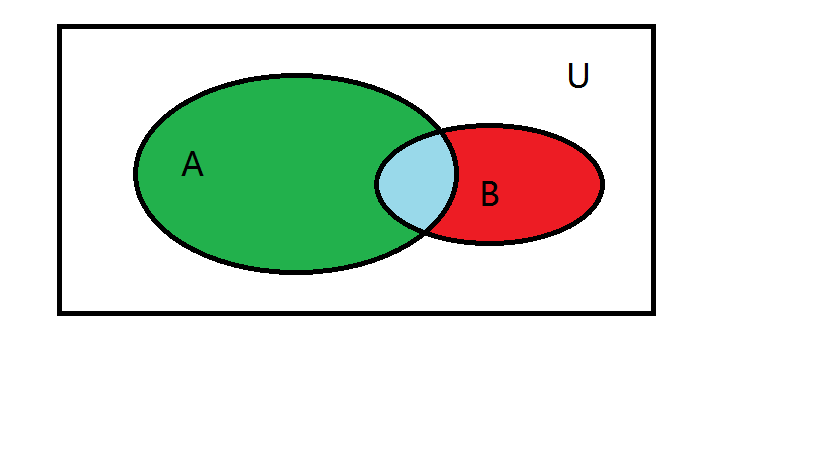
它們兩個集合中含有1,2,3,5這4個元素,不管元素的出現次數,只要元素出現在這兩個集合中。那么說A∪B={1,2,3,5}。 圖中的陰影部分就是A∩B。
交集:以屬於A且屬於B的元素為元素的集合稱為A與B的交(集),記作A∩B(或B∩A),讀作“A交B”(或“B交A”),即A∩B={x|x∈A,且x∈B}
例如,全集U={1,2,3,4,5} A={1,3,5} B={1,2,5} 。那么因為A和B中都有1,5,所以A∩B={1,5} 。
有趣的是;例如在1到105中不是3,5,7的整倍數的數有多少個。結果是3,5,7每項減1再相乘。48個。
基數
無限集:定義:集合里含有無限個元素的集合叫做無限集。
差:以屬於A而不屬於B的元素為元素的集合稱為A與B的差(集)
註:空集包含於任何集合,但不能說“空集屬於任何集合”。
空集也被認為是有限集合。
例如,全集U={1,2,3,4,5} 而A={1,2,5} 那么全集有而A中沒有的3,4就是CuA,是A的補集。CuA={3,4}。
冪集
定義:設有集合A,由集合A所有子集組成的集合,稱為集合A的冪集。
定理:有限集A的冪集的基數等於2的有限集A的基數次冪。
在信息技術當中,常常把CuA寫成~A。
某些指定的對象集在一起就成為一個集合,含有有限個元素叫有限集,含有無限個元素叫無限集,空集是不含任何元素的集,記做Φ。空集是任何集合的子集,是任何非空集的真子集,任何集合是它本身的子集,子集、真子集都具有傳遞性。
『說明一下:如果集合A的所有元素同時都是集合B的元素,則A稱作是B的子集,寫作A B。若A是B的子集,且A不等於B,則A稱作是B的真子集,寫作A B。所有男人的集合是所有人的集合的真子集。』
性質
1.確定性:每一個對象都能確定是不是某一集合的元素,沒有確定性就不能成為集合,例如“個子高的同學”“很小的數”都不能構成集合。這個性質主要用於判斷一個集合是否能形成集合。
2.互異性:集合中任意兩個元素都是不同的對象。如寫成{1,1,2},等同於{1,2}。互異性使集合中的元素是沒有重複,兩個相同的對象在同一個集合中時,只能算作這個集合的一個元素。
3.無序性:{a,b,c}{c,b,a}是同一個集合。
4.純粹性:所謂集合的純粹性,用個例子來表示。集合A={x|x<2},集合A 中所有的元素都要符合x<2,這就是集合純粹性。
5.完備性:仍用上面的例子,所有符合x<2的數都在集合A中,這就是集合完備性。完備性與純粹性是遙相呼應的。
集合有以下性質:若A包含於B,則A∩B=A,A∪B=B
2.描述法﹕常用於表示無限集合,把集合中元素的公共屬性用文字﹐符號或式子等描述出來﹐寫在大括弧內﹐這種表示集合的方法叫做描述法。{x|P}(x為該集合的元素的一般形式,P為這個集合的元素的共同屬性)如:小於π的正實數組成的集合表示為:{x|0<x<π}
3.圖式法(Venn圖)﹕為了形象表示集合,我們常常畫一條封閉的曲線(或者說圓圈),用它的內部表示一個集合。
特性
確定性
給定一個集合,任給一個元素,該元素或者屬於或者不屬於該集合,二者必居其一,不允許有模稜兩可的情況出現。
互異性
一個集合中,任何兩個元素都認為是不相同的,即每個元素只能出現一次。有時需要對同一元素出現多次的情形進行刻畫,可以使用多重集,其中的元素允許出現多次。
無序性
符號表示規則
元素則通常用a,b,c,d或x等小寫字母來表示;而集合通常用A,B,C,D或X等大寫字母來表示。當元素a屬於集合A時,記作a∈A。假如元素a不屬於A,則記作a∉A。如果A和B兩個集合各自所包含的元素完全一樣,則二者相等,寫作A=B。
符號
(2)非負整數集內排除0的集,也稱正整數集,記作N+(或N*)
(3)全體整數的集合通常稱作整數集,記作Z
(4)全體有理數的集合通常簡稱有理數集,記作Q
(6)複數集合計作C
集合的運算:
集合交換律
A∩B=B∩A
A∪B=B∪A
集合結合律
(A∩B)∩C=A∩(B∩C)
(A∪B)∪C=A∪(B∪C)
集合分配律
A∩(B∪C)=(A∩B)∪(A∩C)
A∪(B∩C)=(A∪B)∩(A∪C)
集合德.摩根律
Cu(A∩B)=CuA∪CuB
Cu(A∪B)=CuA∩CuB
集合“容斥原理”
在研究集合時,會遇到有關集合中的元素個數問題,我們把有限集合A的元素個數記為card(A)。例如A={a,b,c},則card(A)=3
card(A∪B)=card(A)+card(B)-card(A∩B)
card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)
集合吸收律
A∪(A∩B)=A
A∩(A∪B)=A
集合求補律
A∪CuA=S
A∩CuA=Φ
德摩根律:A-(BUC)=(A-B)∩(A-C)
A-(B∩C)=(A-B)U(A-C)
~(BUC)=~BU~C
~(B∩C)=~B∩~C
~Φ=E ~E=Φ
模糊集
用來表達模糊性概念的集合,又稱模糊集、模糊子集。普通的集合是指具有某種屬性的對象的全體。這種屬性所表達的概念應該是清晰的,界限分明的。
因此每個對象對於集合的隸屬關係也是明確的,非此即彼。但在人們的思維中還有著許多模糊的概念,例如年輕、很大、暖和、傍晚等,這些概念所描述的對象屬性不能簡單地用“是”或“否”來回答,模糊集合就是指具有某個模糊概念所描述的屬性的對象的全體。
由於概念本身不是清晰的、界限分明的,因而對象對集合的隸屬關係也不是明確的、非此即彼的。這一概念是美國加利福尼亞大學控制論專家L.A.扎德於1965 年首先提出的。