吸收律

在抽象代數中，吸收律是連線一對二元運算的恆等式。

任何兩個二元運算比如 $ 和 %，服從吸收律如果:

a $ (a % b) = a % (a $ b) = a.

運算 $ 和 % 被稱為對偶對。

基本介紹

• 中文名：吸收律
• 外文名：absorption law
• 定義：連線一對二元運算的恆等式
• 套用學科：數學
• 相關術語：結合律
• 所屬領域：數學

簡述

設有某個集合閉合在兩個二元運算下。如果這些運算是交換律、結合律的，並滿足吸收律，結果的抽象代數就是格，在這種情況下這兩個運算有時叫做交和並。因為交換律和結合律經常是其他代數結構的性質，吸收律是格的定義性質。由於布爾代數和 Heyting代數是格，它們也服從吸收律。

因為經典邏輯是布爾代數的模型，直覺邏輯是 Heyting代數的模型，吸收律對分別指示邏輯或和邏輯與的運算。

定義

吸收律對相干邏輯、線性邏輯和亞結構邏輯不成立。在亞結構邏輯情況下，在恆等式的定義對的自由變數之間沒有一一對應。

吸收律的證明

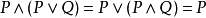
(P ∨ 0) ∧ (P ∨ Q) = P ∨ (0 ∧ Q) = P ∨ 0 = P

(P ∧ 1) ∨ (P ∧ Q) = P ∧ (1 ∨ Q) = P ∧ 1 = P

這裡的 = 號要理解為公式上的邏輯等價。

吸收律對相干邏輯、線性邏輯和亞結構邏輯不成立。在亞結構邏輯情況下，在恆等式的定義對的自由變數之間沒有一一對應。

相關理論

格理論、布爾代數。