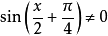基本介紹
- 中文名：恆等式
- 外文名：identities
- 類別：數學概念
- 性質：無論其變數如何取值等式永遠成立
- 套用學科：數學
- 符號：≡
例子,相關聯繫,著名恆等式,乘法公式類,函式類恆等式,其他恆等式,
例子
sin2α+cos2α=1
a2-b2=(a+b)(a-b)
定義
恆等式符號“≡”。
兩個解析式之間的一種關係。給定兩個解析式，如果對於它們的定義域（見函式）的公共部分（或公共部分的子集）的任一數或數組，都有相等的值，就稱這兩個解析式是恆等的。例如x2－y2與(x+y)(x－y) ，對於任一組實數(a,b)，都有a2－b2=(a+b)(a－b)，所以x2－y2與(x+y)(x－y)是恆等的。
相關聯繫
“函式相等”與“恆等式”之間有什麼關係，由“恆等式”能得出“函式相等”嗎？
數學上，恆等式是無論其變數在給定的取值範圍內取何值，等式永遠成立的算式。恆等式有多個變數的，也有一個變數的，若恆等式兩邊就一個變數，恆等式就是兩個 解析式之間的一種關係。給定兩個解析式，如果對於它們的定義域（見函式）的公共部分（或公共部分的子集）的任一數或數組，都有相等的值，就稱這兩個解析式 是恆等的。
y=f(x)與y=g(x)相等，顯然f(x)=g(x)是定義域上的恆等式；若f(x)=g(x)是恆等式，那么y=f(x)與y=g(x)相等嗎？看下面的例子。
1．若
是恆等式，則f(x)=與g(x)=
相等；
2．若
=
是恆等式，則
與
相等.
由此可得如下命題：
1.若y=f(x)與y=g(x)有相同的定義域，對於定義域內的任一個x均有f(x)=g(x)則y=f(x)與y=g(x)是相等函式，同時兩解析式必相同。
2.若y=f(x)與y=g(x)是相等函式，則兩個函式的解析式相同，於是其中的參數都能對應相等。
著名恆等式
歐拉恆等式：
設F(X)=0的n個根X1,X2,……,Xn.對於k∈N，記Sk=X1k+X2k+……+Xnk.則有
C0Sk+C1Sk-1+……+CnSk-n=0 ，當k>0 (N1)
C0Sk+C1Sk-1+……+Ck-1S1+kCk=0 ，當1≤k≤n (N2)
乘法公式類
- 分配律 ab+ac=a(b+c)
- 完全平方
- 三數和平方 (a+b+c)2=a2+b2+c2+2ab+2ac+2bc
- 推廣：(a+b+c+...+n)2=a2+b2+...+n2+2ab+2ac+...+2an+2bc+2bd+...+2(n-1)n
- 和平方(a+b)2=a2+2ab+b2
- 差平方(a-b)2=a2-2ab+b2
平方差(a+b)(a-b)=a2-b2
推廣：an-bn= (a-b)(an-1+an-2b+an-3b2+...a2bn-3+abn-2+bn-1)
