含有等號的式子叫做等式。等式可分為矛盾等式和條件等式。等式兩邊同時加上(或減去)同一個整式,或者等式兩邊同時乘或除以同一個不為0的整式,等式仍然成立。形式是把相等的兩個數(或字母表示的數)用“=”連線起來。
恆等式(identities),數學概念,恆等式是無論其變數如何取值,等式永遠成立的算式。
基本介紹
- 中文名:等式
- 外文名:equation
- 定義:含有等號的式子
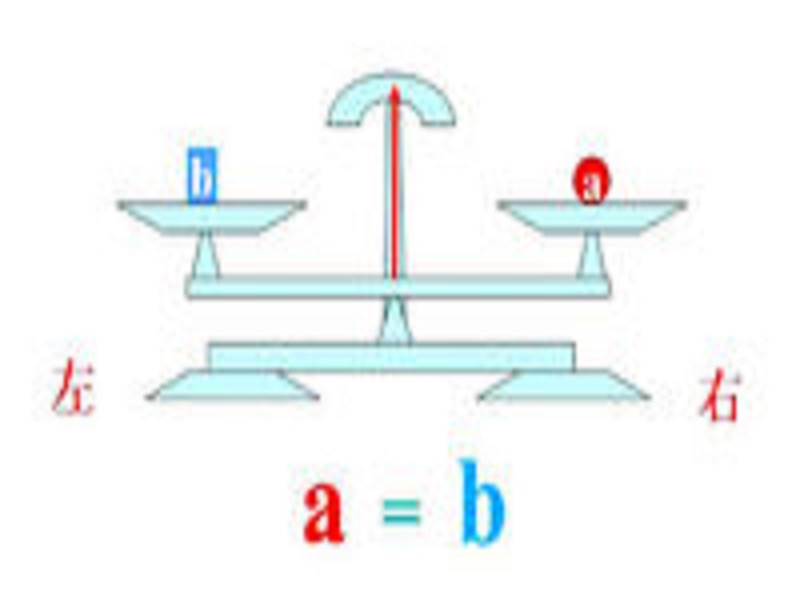
- 性質1:若a=b那么a+c=b+c
- 性質2:若a=b那么a·c=b·c
- 性質3:若a=b那么a2=b2
含有等號的式子叫做等式。等式可分為矛盾等式和條件等式。等式兩邊同時加上(或減去)同一個整式,或者等式兩邊同時乘或除以同一個不為0的整式,等式仍然成立。形式是把相等的兩個數(或字母表示的數)用“=”連線起來。
恆等式(identities),數學概念,恆等式是無論其變數如何取值,等式永遠成立的算式。
含有等號的式子叫做等式。等式可分為矛盾等式和條件等式。等式兩邊同時加上(或減去)同一個整式,或者等式兩邊同時乘或除以同一個不為0的整式,等式仍然成立。形式是...
恆等式(identities),數學概念,恆等式是無論其變數如何取值,等式永遠成立的算式。恆等式成立的範圍是左右函式定義域的公共部分,兩個獨立的函式卻各自有定義域,與x...
如果一個等式,在所討論的範圍里不是對字母的所有允許值都成立,而是僅當字母滿足某些條件時才能使等式成立,這樣的等式叫做條件等式。例如:當x=3時,4x=12;當a=5...
基本等式法是指在本量利基本關係式的基礎上,根據保本點的定義,先求出保本量,再推算保本額的一種方法。在銷售市場上,基本等式法就是在本量利分析的基本公式基礎...
會計等式(Accounting equation) :是揭示會計要素之間內在聯繫的數學表達式,又稱會計方程式或會計恆等式。會計等式有:“資產=負債+所有者權益”“收入-費用=利潤”、...
遞等式,即四則混合運算。在四則混合運算的算式中,按照運算順序把計算過程依次用等式表示出來,這樣的等式叫做遞等式。一步計算直接寫等號如要豎式寫在橫式下面正...
(一)不等式的證明已知A,B,C是三角形的三個內角求證cotA+cotB+cotC>=√3cotA+cotB+cotC=cotA+cotB-cot(A+B)>cotA+cotB-cot(B)=cotA>0...
等式系(system of equations),是一種有窮集合。指由等式演算系統中的等式組成的集合(參見“等式演算”)。是美籍奧地利數學家哥德爾(Godel , K.)為尋找“最一般...
”最根本的標誌是確立了國際通行的‘資產=負債 所有者權益’的平衡等式和相應的會計報表體系,為我國會計制度與國際會計慣例接軌創造了條件。...
赫爾德不等式是數學分析的一條不等式,取名自奧圖·赫爾德(Otto Hölder)。這是一條揭示Lp空間相互關係的基本不等式。赫爾德不等式有許多證明,主要的想法是楊氏不...
”符號替換,恆等式此時退化為貝塞爾不等式。帕塞瓦爾恆等式的這種推廣形式可以用里斯-費歇爾定理加以證明。 [4] 帕塞瓦爾恆等式定理介紹 編輯 畢達...
設f(x)可積且平方可積,則f(x)的傅式係數an和bn的平方構成的級數: 是收斂的,且成立等式: 該等式稱為帕賽瓦爾等式。 ...
柯西-施瓦茨不等式是一個在眾多背景下都有套用的不等式,例如線性代數,數學分析,機率論,向量代數以及其他許多領域。它被認為是數學中最重要的不等式之一。此不等式...
歐拉恆等式也叫做歐拉公式,它是數學裡最令人著迷的公式之一,它將數學裡最重要的幾個常數聯繫到了一起:兩個超越數:自然對數的底e,圓周率π,兩個單位:虛數單位i...
Sellmeier等式是描述特定透明介質中折射率和波長的經驗關係等式。該等式用於確定光在介質中的色散。它於1871年由Wolfgang Sellmeier首次提出。是柯西建立色散模型柯西等式...
Jarzynski恆等式(JE)是一個在統計力學中敘述平衡態和非平衡態之間自由能差異的等式。它是以物理學家Christopher Jarzynski的名字命名的,他在1997年發現了此一恆等式...
(二)含有等號“=”、表示相等關係的式子,就是等式/算式。(三)用運算符號聯結數字而成的式子。例如5×2÷(10-9)=10。算式示例 編輯 2+3 算式...
(1)變換係數:利用等式的基本性質,把一個方程或者兩個方程的兩邊都乘以適當的數,使兩個方程里的某一個未知數的係數互為相反數或相等;(2)加減消元:把兩個方程...
