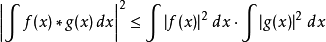柯西—施瓦茨不等式

柯西-施瓦茨不等式是一個在眾多背景下都有套用的不等式，例如線性代數，數學分析，機率論，向量代數以及其他許多領域。它被認為是數學中最重要的不等式之一。此不等式最初於1821年被柯西提出，其積分形式在1859被布尼亞克夫斯基提出，而積分形式的現代證明則由施瓦茲於1888年給出。

基本介紹

• 中文名：柯西-施瓦茨不等式
• 外文名：Cauchy-Buniakowsky-Schwarz
• 提出者：柯西
• 提出時間：1821年
• 推廣者：赫爾曼·阿曼杜斯·施瓦茨
• 推廣者：維克托·布尼亞科夫斯基

簡介

定理（柯西-施瓦茨不等式）：若和是任意實數，則有≤（）（）此外，如果有某個，則上式中的等號若且唯若存在一個實數X使得對於每一個都有時成立。

證明

證明1

平方和絕不可能是負數，故對每一個實數X都有其中，等號若且唯若每一項都等於0時成立。

柯西

數學上，柯西—施瓦茨不等式，又稱施瓦茨不等式或柯西—布尼亞科夫斯基—施瓦茨不等式，是一條很多場合都用得上的不等式，例如線性代數的矢量，數學分析的無窮級數和乘積的積分，和機率論的方差和協方差。不等式以奧古斯丁·路易·柯西（Augustin Louis Cauchy），赫爾曼·阿曼杜斯·施瓦茨（Hermann Amandus Schwarz），和維克托·雅科夫列維奇·布尼亞科夫斯基（Виктор Яковлевич Буняковский）命名。

證明2

施瓦茨

柯西—施瓦茨不等式說，若x和y是實或復內積空間的元素，那么

等式成立若且唯若x和y是線性相關。

柯西—施瓦茨不等式的一個重要結果，是內積為連續函式。

證明3

柯西—施瓦茨不等式有另一形式，可以用范的寫法表示：

套用

實內積空間的情形

注意到y = 0時不等式顯然成立，所以可假設非零。對任意，可知

不等式

現在取值，代入後得到

因此有

復內積空間的情形

證明類上。對任意，可知

現在取值，代入後得到

因此有

特例

對歐幾里得空間，有

對平方可積的復值函式，有

這兩例可更一般化為赫爾德不等式。

在3維空間，有一個較強結果值得注意：原不等式可以增強至等式

利用柯西-比內公式還可得到廣義的柯西不等式如下:

令A,B為兩個m×n矩陣(m>n),則有:

det(A*AT)*det(B*BT)≥(det(A*BT))^2