例如,由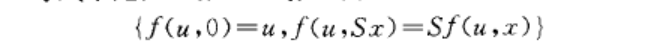
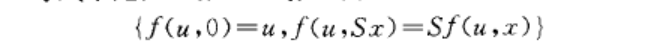
就定義了一個函式f(u,x)=u+二.而等式系則可以含任何有限個“等式”,這種等式的左邊必須形如廣}t},tZ,"..}t.}),其中戶為一個n元函詞,而t為一些項,且其中除了S之外不含其他函詞.上述的遞歸式以及一般的多重遞歸式都由具有這種形狀的遞歸式所組成.若等式系:所含的全體函詞和自由變元為f} , f} , ... , f}及Z,則£記為

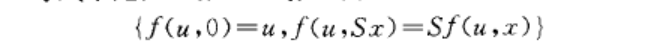

等式系(system of equations),是一種有窮集合。指由等式演算系統中的等式組成的集合(參見“等式演算”)。是美籍奧地利數學家哥德爾(Godel , K.)為尋找“最一般...
等式演算(equation calculus)一種形式系統...... 等式演算(equation calculus)一種形式系統.它最初是由美籍奧地利數學家哥德爾(Godel , K.於1934年為定義一般遞歸函...
埃爾布朗一哥德爾可計算函式(Herbrand-Godelcomputable function)亦稱一般遞歸函式一種等式系可定義函式.是美籍奧地利數學家哥德爾<Godel , K.)根據法國數學家埃爾布朗(...
有窮可定義函式(finitely definable function)亦稱等式系有窮可定義函式.一種由等式系定義的函式.用等式系定義函式的想法最初是由法國數學家埃爾布朗(Herbrand, J....
