集合是指具有某種特定性質的具體的或抽象的對象匯總成的集體，這些對象稱為該集合的元素，數集指就是數的集合。
基本介紹
- 中文名：數集
- 外文名：manifold
- 拼音：shù jí
- 學科：數學
定義,數集類型,性質,數集的起源,
定義
集合是指具有某種特定性質的具體的或抽象的對象匯總成的集體，這些對象稱為該集合的元素，數集就是數的集合。集合的範圍比數集的範圍大，數集只是集合中的一種而已，屬於數集的一定屬於集合，但屬於集合的不一定是數集。
數集類型
數學中一些常用的數集及其記法：
所有負整數組成的集合稱為負整數集，記作Z-；
全體有理數組成的集合稱為有理數集，記作Q；
全體虛數組成的集合稱為虛數集，記作I；
注意：+表示該數集中的元素都為正數，-表示該數集中的元素都為負數，*表示在剔除該數集的元素0（例如，R*表示剔除R中元素0後的數集。即R*=R\{0}=R-∪R+=（-∞，0）∪（0，+∞）。）。
數集與數集之間的關係：
- N*⊊N⊊Z⊊Q⊊R⊊C，
- Z*=Z+∪Z-，
- Q={m/n|m∈Z,n∈N*}={分數}={循環小數},
- R∪I=C，
- R*=R\{0}=R-∪R+=（-∞，0）∪（0，+∞），
- R=R-∪R+∪{0}=R*∪{0}={小數}=Q∪{無理數}={循環小數}∪{非循環小數}。
性質
集合元素具有以下性質：
1、確定性：每一個對象都能確定是不是某一集合的元素，沒有確定性就不能成為集合，例如“個子高的同學”“很小的數”都不能構成集合。這個性質主要用於判斷一個集合是否能形成集合。
2、互異性：集合中任意兩個元素都是不同的對象。
3、無序性：一個集合中，每個元素的地位都是相同的，元素之間是無序的。集合上可以定義序關係，定義了序關係後，元素之間就可以按照序關係排序。但就集合本身的特性而言，元素之間沒有必然的序。
數集的起源
數的概念是從實踐中產生和發展起來的.早在人類社會初期，人們在狩獵、採集果實等勞動中，由於計數的需要，就產生了1，2，3，4等數以及表示“沒有”的數0。自然數的全體構成自然數集N隨著生產和科學的發展，數的概念也得到發展為了解決測量、分配中遇到的將某些量進行等分的問題，人們引進了分數；為了表示各種具有相反意義的量以及滿足記數的需要，人們又引進了負數.這樣就把數集擴充到有理數集Q。如果把自然數集(含正整數和0)與負整數集合併在一起，構成整數集Z。
有些量與量之間的比值，例如用正方形的邊長去度量它的對角線所得的結果，無法用有理數表示，為了解決這個矛盾，人們又引進了無理數。所謂無理數，就是無限不循環小數.有理數集與無理數集合併在一起，構成實數集R。因為有理數都可看作循環小數(包括整數、有限小數)，無理數都是無限不循環小數，所以實數集實際上就是小數集。
因生產和科學發展的需要而逐步擴充，數集的每一次擴充，對數學學科本身來說，也解決了在原有數集中某種運算不是永遠可以實施的矛盾，分數解決了在整數集中不能整除的矛盾，負數解決了在正有理數集中不夠減的矛盾，無理數解決了開方開不盡的矛盾.但是，數集擴到實數集R以後，像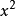
=-1這樣的方程還是無解的，因為沒有一個實數的平方等於-1。由於解方程的需要，人們引入了一個新數i，叫做虛數單位，並由此產生的了複數，隨之產生了複數集。
