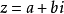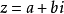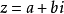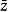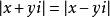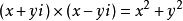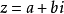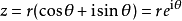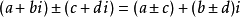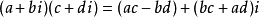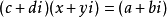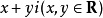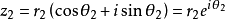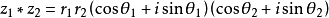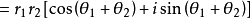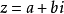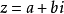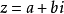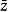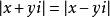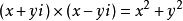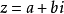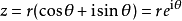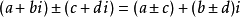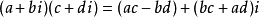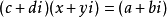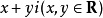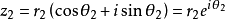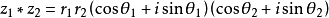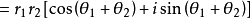複數(數的概念擴展)

我們把形如z=a+bi（a,b均為實數）的數稱為複數，其中a稱為實部，b稱為虛部，i稱為虛數單位。當z的虛部等於零時，常稱z為實數；當z的虛部不等於零時，實部等於零時，常稱z為純虛數。複數域是實數域的代數閉包，即任何復係數多項式在複數域中總有根。 複數是由義大利米蘭學者卡當在十六世紀首次引入，經過達朗貝爾、棣莫弗、歐拉、高斯等人的工作，此概念逐漸為數學家所接受。

基本介紹

• 中文名：複數
• 外文名：complex number
• 表達式：z＝a+bi
• 提出者：Heron of Alexandria
• 提出時間：公元1世紀
• 套用學科：數學
• 相關定理：歐拉公式、棣莫佛定理
• 所屬集合：無序集
• 命名者：Rene Descartes

簡介

我們把形如z=a+bi（a，b均為實數）的數稱為複數，其中a稱為實部，b稱為虛部，i稱為虛數單位。當虛部等於零時，這個複數可以視為實數；當z的虛部不等於零時，實部等於零時，常稱z為純虛數。複數域是實數域的代數閉包，也即任何復係數多項式在複數域中總有根。 複數是由義大利米蘭學者卡當在十六世紀首次引入，經過達朗貝爾、棣莫弗、歐拉、高斯等人的工作，此概念逐漸為數學家所接受。

歷史

最早有關複數方根的文獻出於公元1世紀希臘數學家海倫，他考慮的是平頂金字塔不可能問題。

16世紀義大利米蘭學者卡爾達諾（Jerome Cardan，1501—1576）在1545年發表的《重要的藝術》一書中，公布了一元三次方程的一般解法，被後人稱之為“卡當公式”。他是第一個把負數的平方根寫到公式中的數學家，並且在討論是否可能把10分成兩部分，使它們的乘積等於40時，他把答案寫成，儘管他認為和這兩個表示式是沒有意義的、想像的、虛無飄渺的，但他還是把10分成了兩部分，並使它們的乘積等於40。給出“虛數”這一名稱的是法國數學家笛卡爾（1596—1650），他在《幾何學》（1637年發表）中使“虛的數”與“實的數”相對應，從此，虛數才流傳開來。

數系中發現一顆新星——虛數，於是引起了數學界的一片困惑，很多大數學家都不承認虛數。德國數學家萊布尼茨（1646—1716）在1702年說：“虛數是神靈遁跡的精微而奇異的隱避所，它大概是存在和虛妄兩界中的兩棲物”。然而，真理性的東西一定可以經得住時間和空間的考驗，最終占有自己的一席之地。法國數學家達朗貝爾（1717—1783）在1747年指出，如果按照多項式的四則運算規則對虛數進行運算，那么它的結果總是a+bi的形式（a、b都是實數）。法國數學家棣莫弗（1667—1754）在1722年發現了著名的棣莫佛定理。歐拉在1748年發現了有名的關係式，並且是他在《微分公式》（1777年）一文中第一次用i來表示-1的平方根，首創了用符號i作為虛數的單位。“虛數”實際上不是想像出來的，而它是確實存在的。挪威的測量學家韋塞爾（1745—1818）在1797年試圖給於這種虛數以直觀的幾何解釋，並首先發表其作法，然而沒有得到學術界的重視。

十八世紀末，複數漸漸被大多數人接受，當時卡斯帕爾·韋塞爾提出複數可看作平面上的一點。數年後，高斯再提出此觀點並大力推廣，複數的研究開始高速發展。詫異的是，早於1685年約翰·沃利斯已經在De Algebra tractatus提出此一觀點。

卡斯帕爾·韋塞爾的文章發表在1799年的《Proceedings of the Copenhagen Academy》上，以當今標準來看，也是相當清楚和完備。他又考慮球體，得出四元數並以此提出完備的球面三角學理論。1804年，Abbé Buée亦獨立地提出與沃利斯相似的觀點，即以來表示平面上與實軸垂直的單位線段。1806年，Buée的文章正式刊出，同年讓-羅貝爾·阿爾岡亦發表同類文章，而阿岡的複平面成了標準。1831年高斯認為複數不夠普及，次年他發表了一篇備忘錄，奠定複數在數學的地位。柯西及阿貝爾的努力，掃除了複數使用的最後顧忌，後者更是首位以複數研究著名的。

複數吸引了著名數學家的注意，包括庫默爾（1844年）、克羅內克（1845年）、Scheffler（1845年、1851年、1880年）、Bellavitis（1835年、1852年）、喬治·皮庫克（1845年）及德·摩根（1849年）。莫比烏斯發表了大量有關複數幾何的短文，約翰·彼得·狄利克雷將很多實數概念，例如素數，推廣至複數。

德國數學家阿甘得（1777—1855）在1806年公布了複數的圖象表示法，即所有實數能用一條數軸表示，同樣，複數也能用一個平面上的點來表示。在直角坐標系中，橫軸上取對應實數a的點A，縱軸上取對應實數b的點B，並過這兩點引平行於坐標軸的直線，它們的交點C就表示複數 。象這樣，由各點都對應複數的平面叫做“複平面”，後來又稱“阿甘得平面”。高斯在1831年，用實數組 代表複數 ，並建立了複數的某些運算，使得複數的某些運算也象實數一樣地“代數化”。他又在1832年第一次提出了“複數”這個名詞，還將表示平面上同一點的兩種不同方法——直角坐標法和極坐標法加以綜合。統一於表示同一複數的代數式和三角式兩種形式中，並把數軸上的點與實數一一對應，擴展為平面上的點與複數一一對應。高斯不僅把複數看作平面上的點，而且還看作是一種向量，並利用複數與向量之間一一對應的關係，闡述了複數的幾何加法與乘法。至此，複數理論才比較完整和系統地建立起來了。

經過許多數學家長期不懈的努力，深刻探討並發展了複數理論，才使得在數學領域遊蕩了200年的幽靈——虛數揭去了神秘的面紗，顯現出它的本來面目，原來虛數不“虛”。虛數成為了數系大家庭中一員，從而實數集才擴充到了複數集。

隨著科學和技術的進步，複數理論已越來越顯出它的重要性，它不但對於數學本身的發展有著極其重要的意義，而且為證明機翼上升力的基本定理起到了重要作用，並在解決堤壩滲水的問題中顯示了它的威力，也為建立巨大水電站提供了重要的理論依據。

主要內容

定義

數集拓展到實數範圍內，仍有些運算無法進行（比如對負數開偶數次方），為了使方程有解，我們將數集再次擴充。

在實數域上定義二元有序對z=(a,b)，並規定有序對之間有運算"+"、"×" (記z₁=(a,b),z₂=(c,d))：

z₁ + z₂=(a+c,b+d)

z₁ × z₂=(ac-bd,bc+ad)

容易驗證，這樣定義的有序對全體在有序對的加法和乘法下成一個域，並且對任何複數z，我們有

z=(a,b)=(a,0)+(0,1) × (b,0)

令f是從實數域到複數域的映射，f(a)=(a,0)，則這個映射保持了實數域上的加法和乘法，因此實數域可以嵌入複數域中，可以視為複數域的子域。

記(0,1)=i,則根據我們定義的運算，(a,b)=(a,0)+(0,1) × (b,0)=a+bi，i × i=(0,1) × (0,1)=(-1,0)=-1，這就只通過實數解決了虛數單位i的存在問題。

形如的數稱為複數（complex number)，其中規定i為虛數單位，且（a，b是任意實數）

我們將複數中的實數a稱為複數z的實部（real part）記作Rez=a

實數b稱為複數z的虛部（imaginary part）記作 Imz=b.

當a=0且b≠0時，z=bi，我們就將其稱為純虛數。

複數的集合用C表示，實數的集合用R表示，顯然，R是C的真子集。

複數集是無序集，不能建立大小順序。

複數的模

將複數的實部與虛部的平方和的正的平方根的值稱為該複數的模，記作∣z∣.

即對於複數，它的模

共軛複數

釋義

對於複數，稱複數=a-bi為z的共軛複數。即兩個實部相等，虛部互為相反數的複數互為共軛複數(conjugate complex number）。複數z的共軛複數記作。

性質

根據定義，若(a，b∈R），則=a－bi（a,b∈R）。共軛複數所對應的點關於實軸對稱。兩個複數：x+yi與x-yi稱為共軛複數，它們的實部相等，虛部互為相反數。在複平面上，表示兩個共軛複數的點關於X軸對稱，而這一點正是"共軛"一詞的來源----兩頭牛平行地拉一部犁，它們的肩膀上要共架一個橫樑，這橫樑就叫做"軛"。如果用z表示x+yi，那么在z字上面加個"一"就表示x-yi，或相反。

共軛複數有些有趣的性質：

複數的輻角

概述

在複變函數中，自變數z可以寫成，r是z的模，即r = |z|；θ是z的輻角，記作： Arg（z）。在-π到π間的輻角稱為輻角主值，記作： arg（z）（小寫的A）。

釋義

任意一個不為零的複數的輻角有無限多個值，且這些值相差2π的整數倍。把適合於-π≤θ<π的輻角θ的值，叫做輻角的主值，記作argz。輻角的主值是唯一的。

指數形式：。

運算法則

加法法則

複數的加法法則：設z₁=a+bi，z₂=c+di是任意兩個複數。兩者和的實部是原來兩個複數實部的和，它的虛部是原來兩個虛部的和。兩個複數的和依然是複數。

即

乘法法則

複數的乘法法則：把兩個複數相乘，類似兩個多項式相乘，結果中i²= -1，把實部與虛部分別合併。兩個複數的積仍然是一個複數。

即

除法法則

複數除法定義：滿足的複數叫複數a+bi除以複數c+di的商。

運算方法：將分子和分母同時乘以分母的共軛複數，再用乘法法則運算，

即

開方法則

若zⁿ=r(cosθ+isinθ），則

（k=0，1，2，3…n-1）

運算律

加法交換律：z₁+z₂=z₂+z₁

乘法交換律：z₁×z₂=z₂×z₁

加法結合律：(z₁+z₂)+z₃=z1+(z₂+z₃)

乘法結合律：(z₁×z₂)×z₃=z₁×(z₂×z₃)

分配律：z₁×(z₂+z₃)=z₁×z₂+z₁×z₃

i的乘方法則

i⁴ⁿ⁺¹=i, i⁴ⁿ⁺²=-1, i⁴ⁿ⁺³=-i, i⁴ⁿ=1（其中n∈Z）

棣莫佛定理

對於複數z=r(cosθ+isinθ），有z的n次冪

zⁿ=rⁿ[cos(nθ)+isin(nθ)]　（其中n是正整數）

則

分類

數的分類拓展到複數範圍後，我們對複數範圍的數集做以下分類

複數（a+bi）——集合符號C
—	實數（複數當b=0時）——集合符號R
—	—	有理數——集合符號Q（p/q)
—	—	—	①正有理數——集合符號Q+
—	—	—	—	正整數——集合符號N+或N*
—	—	—	—	—	1
—	—	—	—	—	質數
—	—	—	—	—	合數
—	—	—	—	正分數
—	—	—	①0
—	—	—	①負有理數——集合符號Q-
—	—	—	—	負整數——集合符號Z-
—	—	—	—	負分數
—	—	—	②整數——集合符號Z
—	—	—	—	（自然數）——集合符號N
—	—	—	—	奇數
—	—	—	—	偶數
—	—	—	②分數
—	—	無理數
—	—	—	正無理數
—	—	—	負無理數
—	虛數（b≠0)
—	—	純虛數（a=0)
—	—	混虛數（a≠0）

註：①②代表對“有理數”兩種不同的分類方式。

套用

系統分析

在系統分析中，系統常常通過拉普拉斯變換從時域變換到頻域。因此可在複平面上分析系統的極點和零點。分析系統穩定性的根軌跡法、奈奎斯特圖法（Nyquist plot）和尼科爾斯圖法（Nichols plot）都是在複平面上進行的。

無論系統極點和零點在左半平面還是右半平面，根軌跡法都很重要。如果系統極點

位於右半平面，則因果系統不穩定； 都位於左半平面，則因果系統穩定； 位於虛軸上，則系統為臨界穩定的。如果系統的全部零點和極點都在左半平面，則這是個最小相位系統。如果系統的極點和零點關於虛軸對稱，則這是全通系統。

信號分析

信號分析和其他領域使用複數可以方便的表示周期信號。模值|z|表示信號的幅度，輻角arg(z)表示給定頻率的正弦波的相位。

利用傅立葉變換可將實信號表示成一系列周期函式的和。這些周期函式通常用形式如下的複函數的實部表示：

其中ω對應角頻率，複數z包含了幅度和相位的信息。

電路分析中，引入電容、電感與頻率有關的虛部可以方便的將電壓、電流的關係用簡單的線性方程表示並求解。（有時用字母j作為虛數單位，以免與電流符號i混淆。）

反常積分

在套用層面，複分析常用以計算某些實值的反常函式，藉由復值函式得出。方法有多種，見圍道積分方法。

量子力學

量子力學中複數是十分重要的，因其理論是建基於複數域上無限維的希爾伯特空間。

相對論

如將時間變數視為虛數的話便可簡化一些狹義和廣義相對論中的時空度量 (Metric) 方程。

套用數學

實際套用中，求解給定差分方程模型的系統，通常首先找出線性差分方程對應的特徵方程的所有復特徵根r，再將系統以形為f(t) =e的基函式的線性組合表示。

流體力學

複函數於流體力學中可描述二維勢流(2D Potential Flow）。

碎形

一些碎形如曼德勃羅集合和茹利亞集(Julia set) 是建基於複平面上的點的。

實變初等函式

我們把數學分析中基本的實變初等函式推廣到復變初等函式，使得定義的各種復變初等函式，當z變為實變數x(y=0）時與相應的實變初等函式相同。

注意根據這些定義，在z為任意復變數時，

①．哪些相應的實變初等函式的性質被保留下來

②．哪些相應的實變初等函式的性質不再成立

③．出現了哪些相應的實變初等函式所沒有的新的性質。

復變指數函式

e^a+bi=e^ae^bi=e^a(cosb+isinb)

複數的三角函式

證明：把yi代入泰勒級數，藉助

和來化簡即可；

同理可得a^ix=cos(xlna)+isin(xlna)= (e^ix)^lna

藉助e^ix=cosx+isinx可以方便地證明棣莫佛定理。