複數的模與輻角是複數三角形式表示的兩個基本元素,複數所對應的向量長度稱為複數的幅值,該向量與實軸正方向的夾角為複數的輻角。輻角的大小有無窮多,但是輻角主值唯一確定。利用複數的模和輻角,可以將複數表示成三角表示式和指數表示式,並可以和代數表示式之間互相轉化,以方便討論不同問題時的需要。
基本介紹
- 中文名:輻角
- 外文名:argument
- 方向規定:逆時針為正,順時針為負
- 基本元素:複數的模與輻角
定義
























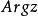


輻角主值

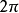











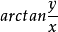

三角表示式和指數表示式







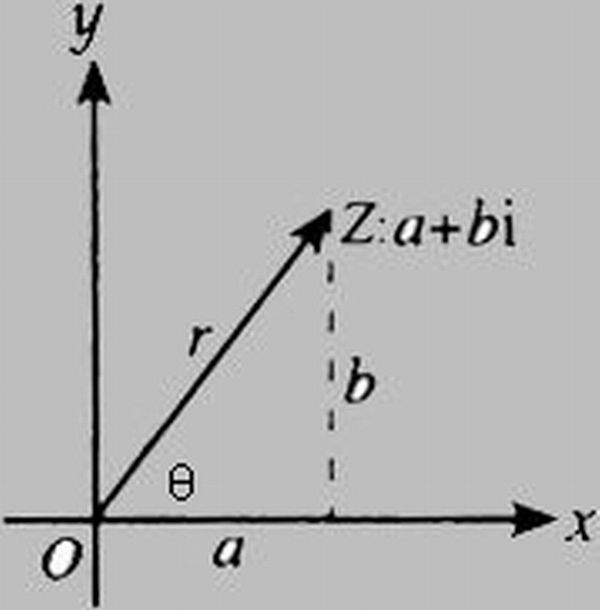
複數的模與輻角是複數三角形式表示的兩個基本元素,複數所對應的向量長度稱為複數的幅值,該向量與實軸正方向的夾角為複數的輻角。輻角的大小有無窮多,但是輻角主值唯一確定。利用複數的模和輻角,可以將複數表示成三角表示式和指數表示式,並可以和代數表示式之間互相轉化,以方便討論不同問題時的需要。

























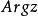



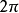











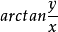








複數的模與輻角是複數三角形式表示的兩個基本元素,複數所對應的向量長度稱為複數的幅值,該向量與實軸正方向的夾角為複數的輻角。輻角的大小有無窮多,但是輻角主...
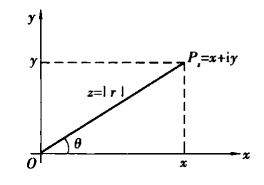
複數的輻角(arg:argument of a complex number )在複變函數中,自變數z可以寫成z=r*(cosθ + i sinθ)。r是z的模,即r = |z|;θ是z的輻角,記作:arg...
在複平面上,複數所對應的向量與x軸正方向的夾角成為複數的輻角,顯然一個複數的輻角有無窮多個,但是在區間(-π,π]內的只有一個,這個輻角就是該向量的輻角...
輻角原理又稱柯西輻角原理,是複變函數中的一個重要原理,即沿著閉曲線C正向繞行一周后輻角argf(z)的改變數除以2π等於f(z)在C的內部的零點和極點個數的差值...
簡介arg: argument of a complex number 複數的輻角 例如: z = r*(cosθ + i sinθ) r是z的模,即:r = |z|; θ是z的輻角,記作:θ = arg(z) ...
,r是z的模,即r = |z|;θ是z的輻角,記作: Arg(z)。在-π到π間的輻角稱為輻角主值,記作: arg(z)(小寫的A)。複數釋義 任意一個不為零的複數 的...
幅角原理是關於解析函式在簡單閉曲線內部的零點個數與極點個數之間的關係的定理。幅角原理是複變函數中的原理,是奈氏判據的數學基礎, 幅角原理用於控制系統的穩定...
▪侵入式虛擬現實互動遊戲的縮寫 ▪複數輻角 ▪精氨酸的縮寫 ▪抗生素抗性基因的縮寫 ▪編程參數argument的縮寫 ▪阿根廷在國際足聯的國家代碼...
幅角定理,是指複變函數中的幅角原理是奈氏判據的數學基礎, 幅角原理用於控制系統的穩定性的判定還需選擇輔助函式和閉合曲線。...
魯歇定理是關於解析函式在區域內部的零點個數的定理,它是輻角原理的一個推論。...... 魯歇定理是關於解析函式在區域內部的零點個數的定理,它是輻角原理的一個推論...
,而輻角不確定。 利用直角坐標與極坐標的關係: ,把 表示成 稱為複數的三角表示式。複數平面2.指數表示式 利用歐拉公式 ,可以得到 ,稱為複數的指數表達式。...
y=Im z。在笛卡爾直角坐標系中,y軸的值為虛部。利用實部和虛部可以判斷兩個複數是否相等,定義共軛複數,計算複數的模和輻角主值。...
