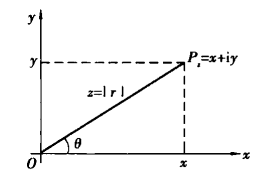
在複平面上,複數所對應的向量與x軸正方向的夾角成為複數的輻角,顯然一個複數的輻角有無窮多個,但是在區間(-π,π]內的只有一個,這個輻角就是該向量的輻角主值,也稱主輻角,記為argz。
基本介紹
- 中文名:輻角主值
- 外文名:principal argument angle
- 別稱:主輻角
- 區間:(-π,π]
定義















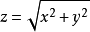
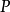







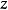


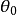
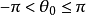
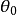
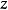



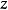
輻角主值的計算





在複平面上,複數所對應的向量與x軸正方向的夾角成為複數的輻角,顯然一個複數的輻角有無窮多個,但是在區間(-π,π]內的只有一個,這個輻角就是該向量的輻角主值,也稱主輻角,記為argz。







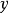








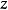

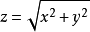
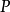







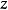


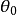
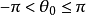
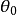
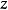







在複平面上,複數所對應的向量與x軸正方向的夾角成為複數的輻角,顯然一個複數的輻角有無窮多個,但是在區間(-π,π]內的只有一個,這個輻角就是該向量的輻角...
複數的模與輻角是複數三角形式表示的兩個基本元素,複數所對應的向量長度稱為複數的幅值,該向量與實軸正方向的夾角為複數的輻角。輻角的大小有無窮多,但是輻角主...
複數的輻角(arg:argument of a complex number )在複變函數中,自變數z可以寫成z=r*(cosθ + i sinθ)。r是z的模,即r = |z|;θ是z的輻角,記作:arg...
簡介arg: argument of a complex number 複數的輻角 例如: z = r*(cosθ + i sinθ) r是z的模,即:r = |z|; θ是z的輻角,記作:θ = arg(z) ...
,r是z的模,即r = |z|;θ是z的輻角,記作: Arg(z)。在-π到π間的輻角稱為輻角主值,記作: arg(z)(小寫的A)。複數釋義 任意一個不為零的複數 的...
y=Im z。在笛卡爾直角坐標系中,y軸的值為虛部。利用實部和虛部可以判斷兩個複數是否相等,定義共軛複數,計算複數的模和輻角主值。...
這裡有一個技巧式的放縮,首先可以確定輻角主值的取值範圍是 ,由於積分 中,被積函式始終為正,因此我們僅討論範圍內的和。 關於 對稱, ,我們可以得到...
他有很強的科研意識和教研能力,《確定複數的輻角主值取值範圍》、《給解題思路培養解題能力》等多篇文章在省級刊物上發表。對青年教師傳幫帶效果顯著。擔任班主任...
共軛複數 共軛虛數 輻角主值 三角形式 代數形式 加法原理乘法原理 幾何圖形 平面圖形 等量代換 度量單位 角平分線互為餘角 互為補角 同旁內角 平行公理 性質定理...
