約當引理

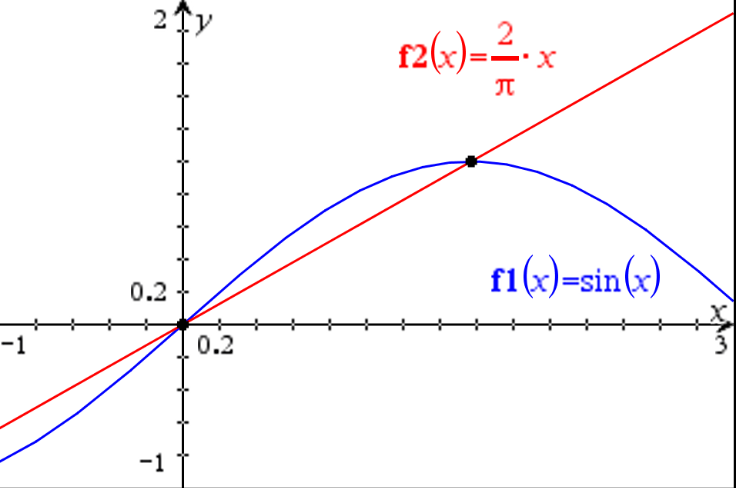
約當(Jordan)引理，也翻譯作諾爾當引理，是複分析中的一條定理。

基本介紹

• 中文名：約當引理
• 外文名：Jordan's Lemma
• 別稱：諾爾當引理
• 套用學科：數學
• 適用領域範圍：複分析，留數定理
• 適用領域範圍：實變反常積分，圍道積分

定律定義

Jordan's Lemma

在複分析中，若複變函數 在閉區域 內可確定其連續且具備極限 , 則對任意 ，有

其中C(R)是以原點為中心，R為半徑的圓弧段。

推導過程

假設在複平面內，積分路徑 ，圓弧段由 起到 結束，有 。利用積分的性質，對求證式左側積分取絕對值，放縮不等式：

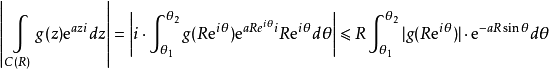
注意到這邊 具有模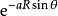

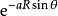
因為 ，因此對任意給定的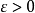 必然存在足夠大的R有 .上式右側積分不大於

這裡有一個技巧式的放縮，首先可以確定輻角主值的取值範圍是 ，由於積分 中，被積函式始終為正，因此我們僅討論範圍內的和。 關於 對稱， ，我們可以得到

在 內，有 . 於是上式右側不大於：

是為所證。

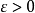
套用領域

Jorden's Lemma與留數定理結合可以解決形如和的積分，其中是多項式函式，並且只需.（即分母多項式次數比分子多項式次數至少大1，否則該積分不會收斂）