基本介紹
- 中文名:平面網路
- 外文名:planar network
- 屬性:網路的一種類型
- 相關概念:網路,拓撲等價,同胚映射等
- 所屬學科:數學(圖論)
基本介紹
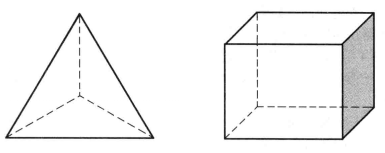 圖1 空間網路示意圖
圖1 空間網路示意圖 圖2 可平面網路示意圖
圖2 可平面網路示意圖 圖3(a)可平面網路的一種實現示意圖
圖3(a)可平面網路的一種實現示意圖 圖3(b)可平面網路的一種實現示意圖
圖3(b)可平面網路的一種實現示意圖相關性質
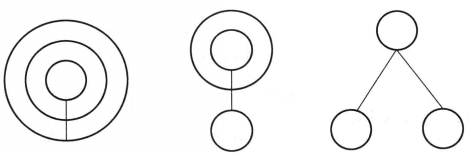 圖3平面網路的幾種不同分布示意圖
圖3平面網路的幾種不同分布示意圖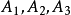
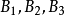
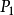
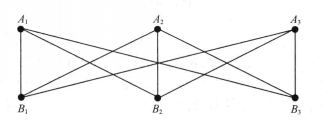 圖4
圖4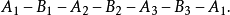
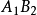
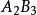
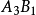
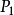
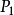
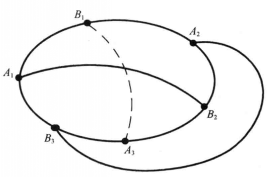 圖5
圖5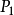
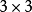
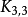
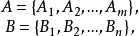

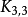
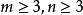

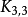

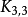
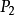
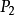
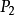
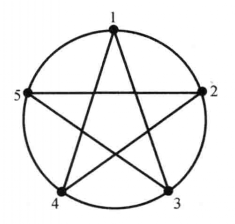 圖6 5點完全網路示意圖
圖6 5點完全網路示意圖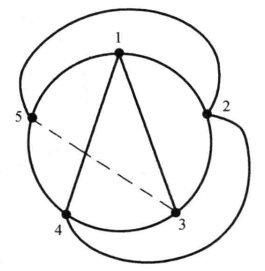 圖7 5點完全網路的平面化示意圖
圖7 5點完全網路的平面化示意圖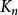
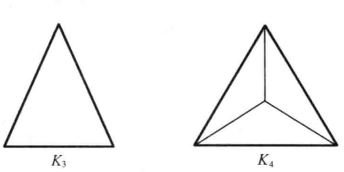 圖8 部分完全網路示意圖
圖8 部分完全網路示意圖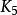
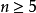
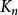
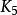
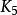
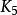
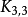
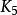
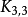
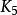
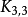
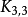
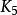
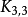
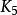

 圖1 空間網路示意圖
圖1 空間網路示意圖 圖2 可平面網路示意圖
圖2 可平面網路示意圖 圖3(a)可平面網路的一種實現示意圖
圖3(a)可平面網路的一種實現示意圖 圖3(b)可平面網路的一種實現示意圖
圖3(b)可平面網路的一種實現示意圖 圖3平面網路的幾種不同分布示意圖
圖3平面網路的幾種不同分布示意圖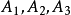
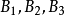
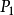
 圖4
圖4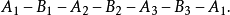
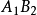
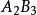
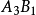
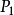
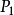
 圖5
圖5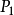
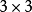
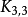
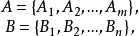

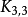
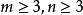

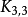

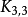
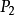
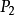
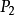
 圖6 5點完全網路示意圖
圖6 5點完全網路示意圖 圖7 5點完全網路的平面化示意圖
圖7 5點完全網路的平面化示意圖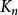
 圖8 部分完全網路示意圖
圖8 部分完全網路示意圖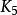
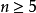
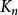
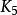
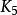
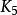
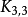
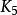
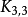
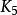
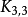
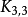
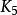
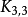
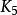
平面網路(planar network)是網路的一種類型,將網路結構畫在平面上,總能使各條支路除了端點以外,不與其他支路相交,這種網路稱為平面網路。實際電路,甚至非常複雜的...
網路的一種類型。將網路結構畫在平面上,無論怎么畫,也得不到平面網路,即網路中總會有某些支路,它除了端點以外,還與其他支路相交,這種網路稱為非平面網路或立體...
報紙、雜誌等傳統媒體通過單一的視覺、單一的維度傳遞信息,相對於電視、網際網路等媒體通過視覺、聽覺等多維度的傳遞信息,而稱作平面媒體。電視、網路等稱作立體媒體。...
根據網路的邏輯結構,將無線感測器網路路由協定分為平面和層次路由。 在平面路由中,所有節點具有相同的地位和功能,節點之間協同工作共同完成感知額外內務。無線感測器網路...
立方米是一家集網站策劃製作,運營最佳化,推廣,後期維護與管理服務和企業宣傳專題策劃,平面設計,多媒體光碟,雜誌,期刊,宣傳冊策劃製作於一體的網路服務公司。...
在LTE的E-UTRAN無線接口協定架構中,將協定棧劃分為用戶平面和控制平面。傳輸信令信息的叫做控制平面。...
LTE接入網稱為演進型UTRAN(Evovled UTRAN,E-UTRAN),相比傳統的UTRAN架構,E-UTRAN採用更扁平化的網路結構。...
《平面生活》是連載於起點中文網的小說,作者是kikofly。...... 葉寧-生命的軌跡,其實只存在於一個平面,平行線永不相交,相交線走過交點……詞條標籤: 網路小說 ,...
方向平面點又稱向量平面點,二維中的圓的圓心,三維中的球體的球心在十維空間中將會是一個平面,對圓周或球面(在十維空間中也是一個平面)產生垂直向下的拉力,拉力...
平面布置圖是建築物布置方案的一種簡明圖解形式,用以表示建築物、構築物、設施、設備等的相對平面位置。繪製平面布置圖常用的方法是平面模型布置法。根據所布置的...
《平面版式設計》是2007年清華大學出版社出版的圖書,作者是席躍良。本書分7章,闡述了平面版式設計的基本理論與當今的發展趨向,對平面版式設計的基本原理、視覺流程、...
平面設計(graphic design)的定義泛指具有藝術性和專業性,以“視覺”作為溝通和表現的方式。透過多種方式來創造和結合符號、圖片和文字,藉此作出用來傳達想法或訊息的...
平面設計工作是一個主觀認定強的創意工作,大部分的平面設計師是通過不斷的自我教育來做進修、提升設計能力。比如,平時就要多注意各式各樣的海報、文宣品、雜誌、...
網路話是伴隨著網路的發展而新興的一種有別於傳統平面媒介的語言形式。它以簡潔生動的形式甫一誕生就得到了廣大網友的偏愛,發展神速。網路語言包括拼音或者英文字母...
平面設計圖是建築工程中不可缺少的步驟之一,用於房屋設計,建築設計,平面設計圖體現了設計師對空間的整體規劃。...
平面設計師認證編輯 鎖定 在讀大學、中專、高國中學生、在職社會青年、社會青年...提供了新的創作工具,加強了對Web網路的支持,其中的ImageReady 2.0可以套用於對...
利用圖像平面結構信息指導塊匹配的圖像修複方法。通過估計平面投影參數,將已知區域分割成平面,並分析相應的結構信息。根據塊偏移和變換的先驗機率將平面結構信息轉換成...
把地理空間抽象為一個二維歐氏平面,以一定規則將點和線連成分布於其間,即構成地理網路。...
英特網,是世界上最大的網路科技術語。聯在英特網上的電腦有數億台。上面的資料、信息數不勝數,所以有人把英特網叫成是信息的海洋、知識的海洋。通用的網址中,...
