同胚

同胚

在拓撲學中，同胚(homeomorphism、topological isomorphism、bi continuous function)是兩個拓撲空間之間的雙連續函式。同胚是拓撲空間範疇中的同構。

基本介紹

  • 中文名：同胚
  • 外文名：homeomorphism
  • 定義：兩個拓撲空間之間的雙連續函式
  • 性質：保持給定空間拓撲性質的映射
  • 套用學科：拓撲學
  • 所屬領域：數學
概念,定義,例子,性質,參見,

概念

在拓撲學中，同胚(homeomorphism、topological isomorphism、bi continuous function)是兩個拓撲空間之間的雙連續函式。同胚是拓撲空間範疇中的同構；也就是說，它們是保持給定空間的所有拓撲性質的映射。如果兩個空間之間存在同胚，那么這兩個空間就稱為同胚的，從拓撲學的觀點來看，兩個空間是相同的。
大致地說，拓撲空間是一個幾何物體，同胚就是把物體連續延展和彎曲，使其成為一個新的物體。因此，正方形和圓是同胚的，但球面和環面就不是。有一個笑話是說，拓撲學家不能區分咖啡杯和甜甜圈，這是因為一個足夠柔軟的甜甜圈可以捏成咖啡杯的形狀。
在拓撲學中，兩個流形，如果可以通過彎曲、延展、剪下(只要最終完全沿著當初剪開的縫隙再重新貼上起來)等操作把其中一個變為另一個，則認為兩者是同胚的。如：圓和正方形是同胚的，而球面和環面就不是同胚的。

定義

兩個拓撲空間{X,TX}和{Y,TY}之間的函式f:X→Y稱為同胚，如果它具有下列性質：
  • f是雙射（單射和滿射）；
  • f是連續的；
  • 反函式f也是連續的（f是開映射）。
滿足以上三個性質的函式有時稱為雙連續。自同胚就是從一個拓撲空間到它本身的同胚。同胚形成了所有拓撲空間的類上的等價關係。所得到的等價類稱為同胚類。

例子

R內的單位圓盤D和單位正方形是同胚的。
開區間(−1, 1)與實直線R同胚。
積空間S× S與二維環面同胚。
每一個一致同構和等距同構都是同胚。
任何二維球面去掉一個點都與R中的所有點所組成的集合（二維平面）同胚。
設A為一個有單位的交換環，並設S為A的乘法子集。那么Spec
與
同胚。
當
時，
不與
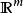同胚。
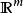
一個連續和雙射但不是同胚的函式的例子，是把半開區間 [0,1)纏繞到圓上的映射。在這個情況中，逆映射雖然存在，但不是連續的。

性質

  • 同胚是拓撲空間範疇中的同構。因此，兩個同胚的複合映射也是同胚，且所有自同胚X→X形成了一個群，稱為X的自同胚群，通常記為Homeo(X)。
  • 兩個同胚的空間具有相同的拓撲性質。例如，如果其中一個是緊空間，那么另外一個也是緊空間；如果其中一個是連通空間，那么另外一個也是連通空間，等等。然而，這不能推廣到通過度量所定義的性質；如果兩個度量空間是同胚的，那么仍然有可能其中一個是完備的，而另外一個不是。
  • 同胚既是開映射又是閉映射，也就是說，它把開集映射到開集，把閉集映射到閉集。
  • 每一個S1的自同胚都可以延伸到整個圓盤D2的自同胚。

參見

熱門詞條

聯絡我們