基本介紹
定義




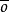






正式表述
目的
性質










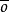











在抽象代數(abstract algebra)中,同構(isomorphism)指的是一個保持結構的雙射(bijection)。在更一般的範疇論語言中,同構指的是一個態射,且存在另一個態射,使得...
同構現象,是視覺美學中的一個概念,就是指某個共同的元素為多個元素所共用的現象,是奇妙的視錯覺現象。構成的新圖形並不是原圖形的簡單相加,而是一種超越或突變,...
若同態映射 f 是一個雙射,則稱 f 為 G 到 G’ 的同構映射,這時稱群 G 和 G’ 同構。...
分散式資料庫管理系統按局部DBMS的類型分類,可分為二類:同構型系統和異構型系統。[2] 同構型(也稱均質型)系統是指系統中每個結點上的資料庫類型都相同,即它們支持...
同構基本定理,即同態基本定理,由埃米·諾特提出。包含三個定理,在泛代數領域有廣泛的套用,證明了一些自然同構的存在性。...
射m:V→V1,使得對所有的x,y∈V均有xy∈E等價於m(x)m(y)∈E1,則稱G和G1是同構的,這樣的一個映射m稱之為一個同構,如果G=G1,則稱他為一個自同構...
同構說(гипотезаосемантико-синтакси-ческомизоморфизме)認為,句子的語義位框架模式與句法位諧配模式之間...
描述 模型同構(isomorphism of models)模型論術語.指兩模型間的一種等價關係.語言丫中的模型}l=CA,{r},}f},{:})和.}= CB,{、},fig},{d})同構(記為...
在數學中,特別是黎曼幾何跟微分流形的理論里,音樂同構(Musical isomorphism 或典範同構 canonical isomorphism)是指(偽)黎曼流形 M 的切叢 TM 與餘切叢T*M 之間...
異形同構是將兩種以上的形象素材重新構成,為廣告設計中圖形創意的一種表現形式。...... 異形同構是將兩種以上的形象素材重新構成,為廣告設計中圖形創意的一種表現形式...
設E與F為兩個群胚,兩個么半群,兩個群,兩個環,兩個向量空間,兩個代數或兩個酉代數。稱從E到F中的映射f是同構,如果f有逆映射,並且f與f-1是兩個同態。...
同構證明方法是一種證明方法。同態和同構是布爾巴基學派提出的重要概念,它是對於結構之間關係的描述。雖然同構概念提出較晚,但其意義是極其深遠的。同構不僅是數學的...
柯里-霍華德同構是指電腦程式和數學證明之間的緊密聯繫;即函式的類型相當於命題,函式的實現相當於證明。這種對應也叫做柯里-霍華德對應、公式為類型對應或命題為...
拓撲同構(topological isomorphism)拓撲群之間的同構概念.設G G:都是拓撲群,若筍:G,~GZ是群同構,而且筍和抓‘都是連續函式,則稱筍是拓撲同構,稱兩個群G,和...
同構圖形,是指將兩個或兩個以上的圖形通過圖形設計的組合、嫁接等處理手段組合在一起,共同構成一個新圖形,並且要傳達出一個新的意義。這個新圖形並不是原圖形的...
世界上一切事物都具有相同的或者說是相類似的系統結構叫做事物的同構性。舉個最簡單的例子,八大行星圍繞太陽轉動,電子圍繞質子轉動是這兩個事物的同構性;已開發國家...
模同構是一種特殊的模同態,假設f是模M到模N的同態,若f時一一的並且是映上的,則f為模M到模N的同構。兩個同構的模,從模的結構來看,它們沒有什麼區別。模...
同態與同構,是近世代數系統中的概念,是學習其他相關課程的基礎概念。...... 同態與同構,是近世代數系統中的概念,是學習其他相關課程的基礎概念。中文名 同態與同構...
同構在抽象代數(abstract algebra)中,同構(isomorphism)指的是一個保持結構的雙射(bijection)。在更一般的範疇論語言中,同構指的是一個態射,且存在另一個態射,...
設計同構(isomorphism of designs)同類型區組設計間的一種關係.設(X,.})與(X}, oy,)是兩個((v , k , .})-BIBD,若存在X到X'的一一映射,把,中每個...
自同構群(group of automorphisms)是一種重要的幾何變換群。是幾何學分類的依據。自同構群一種特殊的群。指群自身的映射所構成的群。群G的所有自同構在映射的...
同構定理(isomorphism theorem)類域論的重要定理.該定理斷言:數域k的希爾伯特類域kH的伽羅瓦群G(kH/k)與k的理想類群同構.這一定理到一般類域上有推廣. ...
職責同構是指不同層級的政府在縱向間職能、職責和機構設定上的高度統一、一致。這不僅是對中國縱向政府間關係總特徵的一個理論概括,而且在國家的法律和制度基礎、...
同構網路計算系統now或cow首先興起,接著很快湧現出異構網路計算系統,從而使異構計算近年來成為並行/分布計算領域中的主要研究熱點之一。...
