對於一個集合A,A中定義一個閉合運算○,存在一個A與A之間的映射φ ,若φ為一雙射,且對於A內任意元素a,b都有φ(a○b)=φ(a)○φ(b)則這個映射φ 叫做一個對於○ 來說的A的自同構(automorphism)。
基本介紹
- 中文名:自同構
- 外文名:automorphism
- 釋義:數學對象對其本身的一個同構
- 定義關鍵:數序對象
- 一級學科:數學
- 二級學科:代數數論
定義
例子
○ | 1 | 2 | 3 |
1 | 3 | 3 | 3 |
2 | 3 | 3 | 3 |
3 | 3 | 3 | 3 |
自同構群
不完全圖的自同構
 圖1
圖1 圖2
圖2



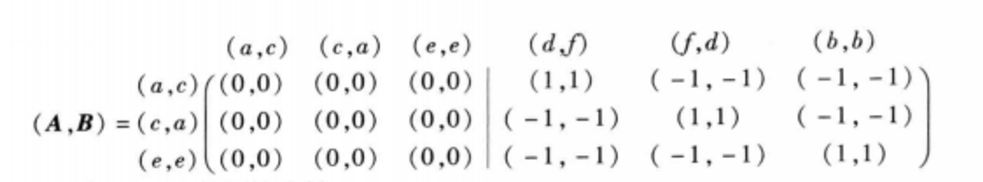
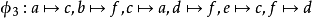

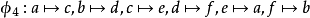





對於一個集合A,A中定義一個閉合運算○,存在一個A與A之間的映射φ ,若φ為一雙射,且對於A內任意元素a,b都有φ(a○b)=φ(a)○φ(b)則這個映射φ 叫做一個對於○ 來說的A的自同構(automorphism)。
○ | 1 | 2 | 3 |
1 | 3 | 3 | 3 |
2 | 3 | 3 | 3 |
3 | 3 | 3 | 3 |
 圖1
圖1 圖2
圖2



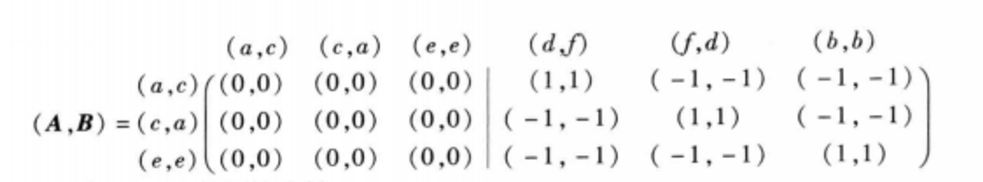
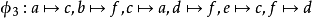

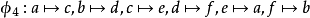




存在一個A與A之間的映射φ ,若φ為一雙射,且對於A內任意元素a,b都有φ(a○b)=φ(a)○φ(b)則這個映射φ 叫做一個對於○ 來說的A的自同構(...
自同構群(group of automorphisms)是一種重要的幾何變換群。是幾何學分類的依據。自同構群一種特殊的群。指群自身的映射所構成的群。群G的所有自同構在映射的...
運算○,存在一個A與A之間的映射φ ,若φ為一雙射,且對於A內任意元素a,b都有φ(a○b)=φ(a)○φ(b)則這個映射φ 叫做一個對於○ 來說的A的自同構。...
它是一個單一同態,若這個同態又是滿同態,也就是F=Fp,則F是完備域,若π是單一同態,且是滿同態,則π是F的一個自同構,稱為弗羅貝尼烏斯自同構(Frobenius ...
對合自同構(involutive automorphism)聯繫李群與黎曼對稱空間的紐帶.李群‘的二階自同構。...
度結構的自同構(automorphism of degrees'structure)遞歸論的基本概念之一指度結構到其自身的一一保序映射.若f為羅~少的一一映射,且對任何x,yE},x<yHf(x)<f...
擴域自同構(automorphism of an extensionfield)伽羅瓦理論的重要概念,它是建立擴域塔與子群塔之間對應關係的主要工具.設K,L是F的兩個擴域,K到L上保持F中元不...
華羅庚定理原意是:除環的半自同構,除了自同構和反自同構以外,再也沒有其它的了。...... 華羅庚定理原意是:除環的半自同構,除了自同構和反自同構以外,再也沒...
乘子(multiplier)亦稱乘數,是一類特殊的自同構。設D為群G的一個(v,k,λ)差集,G的運算以加法記,α為G的一個自同構。若存在a,b∈G,使Dα=a+D+b,則稱...
“華氏定理”是我國著名數學家華羅庚的研究成果。 華氏定理為:體的半自同構必是自同構自同體或反同體。 數學家華羅庚關於完整三角和的研究成果被國際數學界稱為“...
自同構是數學結構的元素的一個保持結構的排列。設E為群胚,么半群,群,環,向量空間,代數或酉代數。從E到其自身上的同構稱為E的自同構。...
在數學的群論中,完備群(又稱完全群,不過完全群也可以指另一種群)是指如下的一種群G:G是無中心群,並且G的所有自同構都是內自同構,也就是說G有平凡外自...
賦以合成法則(f,g)↦g°f後,E的自同構集是一個群,自然地稱為E的自同構群,記為Aut(E).例如,設E為交換體K上的向量空間. E的同位相似是自同構,當且...
《弧傳遞圖與邊本原圖》是2012年北京交通大學據此授予博士學位證書,主要講了弧傳遞圖本原圖Cayley圖陪集圖自同構群。...
的自同態(或自同構)。若序同態 是滿射,則稱偏序集P與Q同態,記作 ;若 是序同構,則稱P與Q同構,記作 :若P與Q的某一個子偏序集同構,則稱偏序集P可同構嵌入...
設K是域,且當1.=BZ或F、時K是特徵2的完全域;當L=GZ時K是特徵3的完全域,若G=L(K)是K上L型謝瓦萊群,則存在G的自同構g,稱為圖自同構,將每個基礎根...
在射影平面上取一條非退化的虛二階曲線k:x²₁+x²₂+x²₃=0作為絕對形,關於虛二階曲線k的自同構變換稱為橢圓射影運動。具有公共絕對形的橢圓射...
1圓周C′自映射的拓撲2圓周上的擴張映射,一個典型的例子及其結構穩定性3圓周上擴張映射的一般情形4擴張映射的性質第五章環面的雙曲自同構1環面自映射的提升...
如果V是在域F上的向量空間,V的一般線性群,寫為GL(V)或Aut(V),是V的所有自同構的群,就是說所有自同構V→V的集合,和與之一起的函式複合作為群運算。如果V...
