在數學中,一般線性群是指基域K上n×n 可逆矩陣全體組成的矩陣乘法群。
在任何域 F或環 R上的 n 次一般線性群是帶有來自 F(或 R)的元素的 n×n 可逆矩陣的群,帶有矩陣乘法作為群運算。典型符號是 GLn(F)或 GL(n, F),如果域是自明的也可簡寫為 GL(n)。
基本介紹
- 中文名:一般線性群
- 外文名:general linear group
- 學科領域:數學 代數學 群論
- 別稱:全線性群
- 性質:典型群
- 記號:GL(V)
簡介
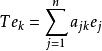
定義
群
典型群
相似群
酉群
辛群
正交群
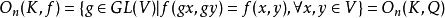
在數學中,一般線性群是指基域K上n×n 可逆矩陣全體組成的矩陣乘法群。
在任何域 F或環 R上的 n 次一般線性群是帶有來自 F(或 R)的元素的 n×n 可逆矩陣的群,帶有矩陣乘法作為群運算。典型符號是 GLn(F)或 GL(n, F),如果域是自明的也可簡寫為 GL(n)。
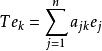
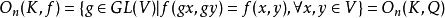
在數學中,一般線性群是指基域K上n×n 可逆矩陣全體組成的矩陣乘法群。在任何域 F或環 R上的 n 次一般線性群是帶有來自 F(或 R)的元素的 n×n 可逆矩陣...
一般線性群亦稱全線性群。一類重要的典型群。若V是體K上n維右線性空間,則V上全體可逆線性變換在映射的乘法下構成一個群,稱為V上的一般線性群或全線性群,記為...
含義 數學概念 例子 置換群,循環群,一般線性群等 相關定義 阿貝爾群、同態、共軛類等 性質 封閉性、結合律、單位元和逆元 目錄...
典型群是一類重要的群。一般線性群、酉群、辛群、正交群,以及它們的換位子群、對中心的商群等統稱為典型群。實數域和複數域上的典型群是李群的重要例子,它們的...
代數群的閉子簇若同時也是個子群,則稱為閉子群,它仍是個代數群。代數群關於它的正規閉子群的商群也是個代數群。例如,K上n級一般線性群(K上n級非奇異矩陣...
代數群的閉子簇若同時也是個子群,則稱為閉子群,它仍是個代數群。代數群關於它的正規閉子群的商群也是個代數群。例如,K上n級一般線性群(K上n級非奇異矩陣...
代數群的閉子簇若同時也是個子群,則稱為閉子群,它仍是個代數群。代數群關於它的正規閉子群的商群也是個代數群。例如,K上n級一般線性群(K上n級非奇異矩陣...
數學中的"一般線性群"符號是GL(n,F),群里的元素是域F上的n階可逆矩陣。 ...... 數學中的"一般線性群"符號是GL(n,F),群里的元素是域F上的n階可逆矩陣...
所謂仿射聯絡應該是以仿射變換群為結構群的主叢上的聯絡,在以一般線性群為結構群的主叢上的聯絡稱為線性聯絡。套用比較廣泛的是線性聯絡,特別是在與一般線性群的...
長於代數環上的線性群。與人合作建立了非平衡統計物理的一般機率模型,開展隨機場與無窮質點馬爾可夫過程的研究。“無窮質點馬爾可夫過程與Q過程”1985年獲國家教委科技...
高階K群(higher K-group)格羅滕迪克群(K。群)、懷特海群(K:群)、施坦貝格群的中心(Kz群)的推廣及一般化.代數K理論的重要研究對象.n妻3時,K。群稱為高...
在V 上取一組基,把線性變換 ρ(g) 在此基下的矩陣記作 T(g),則 g→ T(g) 是 G 到一般線性群 GL(n,K) 內的同態,它稱為 G 的矩陣表示。...
典型纖維為實向量空間Rn,且其結構群為通常的一般線性群GL(n,R),這樣構成的向量叢稱為實矢量叢。...
